Ссылка на задачу — 3394. Check if Grid can be Cut into Sections.
📌 Описание задачи
Дано квадратное поле n×n, в котором размещены непересекающиеся прямоугольники.
Необходимо определить, можно ли сделать две горизонтальные или две вертикальные разрезки, чтобы:
- В каждой из трёх частей оказалось хотя бы по одному прямоугольнику.
- Каждый прямоугольник остался ровно в одной части.
Если такие разрезки возможны, вернуть true, иначе — false.
Пример
- Входные данные:
n = 5, rectangles = [[1,0,5,2],[0,2,2,4],[3,2,5,3],[0,4,4,5]]
- Ответ:
true
- Визуальное пояснение:
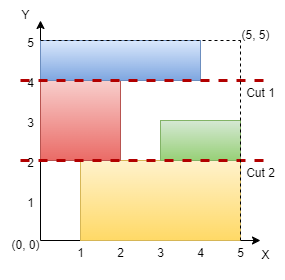
💡 Идея
Поскольку прямоугольники не пересекаются, возможные разрезки должны полностью разделять их на независимые группы.
Мы спроектируем прямоугольники на каждую ось. Если полученные отрезки отсортировать по координатам и просканировать их, можно определить количество неперекрывающихся сегментов, это позволит понять, возможно ли корректное разбиение.
Читать дальше →
ответить
Ссылка на задачу — 3108. Minimum Cost Walk in Weighted Graph.
📌 Описание задачи
- Дан неориентированный взвешенный граф с
n вершинами и m рёбрами.
- Каждое ребро представлено тройкой
[u, v, w], означающей, что существует ребро между u и v с весом w.
- Определим стоимость пути между двумя вершинами как битовое
AND всех рёбер, пройденных на пути (вершинам в таком пути разрешено повторяться).
- Для каждого запроса
[s, t] требуется найти минимальную AND-стоимость пути между s и t.
- Если пути не существует, ответ
-1.
Пример
- Входные данные:
n = 5; edges = [[0,1,7],[1,3,7],[1,2,1]]; query = [[0,3],[3,4]]
- Результаты:
[1, -1]
- Объяснение:
- Наилучший путь от
0 до 3: 0 → 1 → 2 → 1 → 3.
- Путей из
3 в 4 не существует.
- Графическая интерпретация:
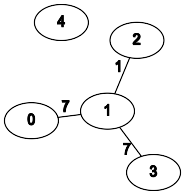
💡 Идея
- Так как каждое новое ребро пути его стоимость не увеличивает, то внутри каждой компоненты связности стоимость минимального пути будет одинаковой (достаточно определить путь, проходящий через все рёбра компоненты связности).
Читать дальше →
1 ответ
Ссылка на задачу — 2115. Find All Possible Recipes from Given Supplies.
В этой задаче для эффективного решения важно не только выбрать эффективный алгоритм, но и аккуратно разложить строки по необходимым структурам данных, избежать лишних копирований и обеспечить ясную картину ownership'a за объектами.
📌 Описание задачи
- У нас есть список рецептов, каждому из которых соответствует список ингредиентов.
- Некоторые ингредиенты могут быть другими рецептами, а некоторые — изначально доступны (входят в список запасов).
- Нужно определить, какие рецепты можно приготовить, имея начальные запасы и возможность использовать приготовленные рецепты.
💡 Идея
Используем рекурсивный DFS для проверки доступности рецептов.
Чтобы избежать повторных вычислений, применяем мемоизацию (кеширование уже проверенных результатов).
Вместо хранения графа явным образом, мы используем индексирование рецептов и проходим по их списку ингредиентов.
🔍 Детали подхода
- Предобработка входных данных:
- Создаём хеш-таблицу для быстрого доступа к индексу каждого рецепта.
- Добавляем начальные запасы в кеш доступных ингредиентов.
Читать дальше →
ответить
Ссылка на задачу — 2401. Longest Nice Subarray.
📌 Описание задачи
Дан массив nums, состоящий из целых чисел.
Нужно найти наибольший подмассив, в котором ни одна пара чисел не имеет общих установленных битов
(т.е. их побитовое И (&) равно 0).
Пример
- 📥 Вход:
nums = [1, 3, 8, 48, 10]
- 📤 Выход:
3
- 🔍 Пояснение: Наибольший "красивый" подмассив:
[3, 8, 48], так как:
3 & 8 = 03 & 48 = 08 & 48 = 0- Никакой больший подмассив не удовлетворяет условиям.
💡 Идея
Будем решать задачу в чистом функциональном стиле, используя технику скользящего окна.
- Расширяем окно вправо, если
nums[right] не конфликтует с текущим битовым множеством.
- Сжимаем окно слева, если появляется конфликт.
- Отслеживаем текущее битовое множество (
cur_bitset), обновляя его при изменении окна.
Читать дальше →
1 ответ
Следственное бюро Братьев Пилотов сообщает:
Во время загрузки страницы на сервере произошло нечто неладное.
Подозреваются:
- 🐧 Пингвин, слишком усердно ковырявшийся в настройках
- 🧠 Шеф, перепутавший кнопку "запустить" и "самоуничтожить"
- 🐈 Кот Мусипусик, проливший молоко на кабель

🕵️ Что произошло?
Сервер сломался, испугался или просто ушёл пить чай.
К счастью, Братья Пилоты уже ведут расследование!
🧩 Что делать?
- Вернитесь на главную — там безопаснее.
- Подождите пару минут и обновите страницу.
- Или напишите нам, если заметили что-то подозрительное: 📩 Связаться со службой
"Это вам не простая ошибка. Это — ошибка с усами!"
— Шеф (3 минуты назад, после падения сервера).
ответить
Любимые факты об английском. Просто так, может, вы тоже порадуетесь. Ничего сверхъестественного, но удивляет, когда задумаешься.
"Ученик" ("школьник") по-английски "зрачок". То есть, "я весь внимание", буквально.
По-английски в радуге тоже семь цветов. Но это другие семь цветов. Синий и голубой ведь один и тот же цвет, а вот фиолетовые бывают разные.
"Государство" по-английски звучит примерно как "состояние дел". "Failed state" это не когда из крана перестает течь вода, а террористы мародерят в пригородах столицы, это просто констатация того, что некое "состояние дел" перестало самовоспроизводиться. "State", впрочем, даже в узком значении "состояние дел, связанное с управлением людьми на определенном куске земного шара" бывает не только таким, к которому мы привыкли (то, скорее, "nation state").
Слова "gore" в русском языке нет, хотя понятие, казалось бы, абсолютно базовое.
Слово "убийца" можно перевести на английский по меньшей мере 8 разными способами (slayer, killer, murderer, assassin, hitman, triggerman, manslayer, cutthroat). Наверное, есть больше. По-русски есть ещё душегуб, головорез (хотя он, скорее, thug, чем cutthroat) и позаимствованный "киллер". Вроде бы, всё?
Слова "зависть" и "ревность" почти взаимозаменяемы и носители языка считают нужным многословно пояснять разницу между ними, причем "зависть" (по крайней мере, в подобных заметках) считается более позитивным чувством. С другой стороны, "ревность" это вообще-то два разных слова, jealousy и insecurity, в зависимости от того, обладает ли испытывающий это чувство предметом вожделения в настоящий момент. "Insecurity", впрочем, это далеко не только "ревность". Сложна.
"Интеллигенция" по-английски "intelligentsia". В XXI веке употребляется далеко не только (и уже, по-моему, не столько) в значении "...в СССР", хотя раньше слово с таким значением почему-то никому не требовалось.
2 ответа
Ссылка на задачу — 3480. Maximize Subarrays After Removing One Conflicting Pair.
📌 Описание задачи
- Дан массив чисел от
1 до n и список конфликтных пар conflicting_pairs,
где каждая пара [a, b] запрещает подотрезки[1, n] , в которых a и b встречаются совместно.
- Требуется удалить ровно одну конфликтную пару так,
чтобы получить максимальное количество подотрезков из [1, n], удовлетворяющих оставшимся ограничениям.
Пример
- Входные параметры:
n = 5, conflictingPairs = [[1,2],[2,5],[3,5]]
- Ответ:
12
- Объяснение:
Удаляем [1, 2] из массива конфликтных пар. Остаются: [[2, 5], [3, 5]].
Всего 12 подотрезков удовлетворяют условию не содержать одновременно 2 и 5 или 3 и 5.
Это отрезки: 1..1, 1..2, 1..3, 1..4, 2..2, 2..3, 2..4, 3..3, 3..4, 4..4, 4..5, 5..5
💡 Идея
- Ключевое наблюдение заключается в том, что конфликтные пары создают ограничения на диапазоны, ограничивая допустимые подотрезки.
Читать дальше →
ответить
Ссылка на задачу — 2226. Maximum Candies Allocated to K Children.
📌 Описание задачи
Дан массив candies, где candies[i] — это количество конфет в i-й куче. Нужно раздать конфеты k детям так, чтобы каждый ребёнок получил одинаковое количество конфет и все конфеты одного ребёнка были взяты из одной кучи.
Требуется найти максимальное возможное количество конфет, которое может получить каждый ребёнок.
💡 Идея
Перебор всех возможных вариантов распределения неэффективен. Вместо этого воспользуемся бинарным поиском по ответу:
- Минимальное возможное количество конфет на ребёнка —
0,
- Максимальное —
total_candies / k (тут total_candies — общее количество конфет).
Будем проверять, можно ли выдать каждому ребёнку candies_per_child конфет.
Если да, увеличиваем candies_per_child, иначе уменьшаем.
🛠 Подробности метода
- Вычисляем
total_candies — суммарное количество конфет.
- Условие быстрого выхода: если
total_candies < k, сразу возвращаем 0.
- Определяем предикат
can_share, который проверяет, можно ли распределить candies_per_child конфет на k детей.
Читать дальше →
ответить
Ссылка на задачу — 3356. Zero Array Transformation II.
📝 Описание задачи
Дан массив nums длины N и список запросов queries, каждый из которых задаётся как [li, ri, vali]. Запрос означает, что значения в диапазоне [li, ri] можно уменьшить на любое число от 0 до vali независимо друг от друга.
Нужно найти минимальное число первых запросов k, после которых nums может превратится в массив, состоящий только из нулей. Если это невозможно — вернуть -1.
💡 Идея
Вместо того, чтобы изменять nums напрямую, будем хранить массив последовательных изменений к декременту (updates). Он позволяет эффективно применять диапазонные операции без лишних вычислений.
Чтобы минимизировать количество обработанных запросов, будем использовать жадную стратегию обработки запросов:
- Обрабатываем
nums последовательно
- Для каждой позиции
i, если nums[i] ещё не стал 0, пытаемся применить минимально возможное число новых запросов из списка.
⚙️ Детали подхода
- Используем массив
updates (N+1 элементов), где updates[i] хранит последовательные изменения к декременту значений.
Читать дальше →
ответить
Ссылка на задачу — 3479. Fruits Into Baskets III.
📌 Описание задачи
У нас есть два массива:
fruits[i] — количество фруктов i-го типаbaskets[j] — вместимость j-й корзины
Нужно распределить фрукты по корзинам слева направо по следующим правилам:
- Каждый тип фруктов должен быть помещён в самую левую подходящую корзину,
где вместимость соответствует (≥) количеству этих фруктов.
- Одна корзина может содержать только один тип фруктов.
- Если фрукт не удалось разместить — он остаётся неразмещённым.
Требуется вернуть количество неразмещённых фруктов.
💡 Идея
Используем дерево отрезков для эффективного поиска первой подходящей корзины.
Это позволит быстро находить и обновлять вместимость корзин за логарифмическое время, что намного быстрее наивного перебора.
🔍 Подробности подхода
- Построение дерева отрезков 🌳:
- Создаём дерево отрезков для максимумов на интервалах, инициализируюя его вместимостями корзин.
Читать дальше →
ответить
Ссылка на задачу — 3306. Count of Substrings Containing Every Vowel and K Consonants II.
📌 Условие задачи
Дана строка word и неотрицательное число k.
Необходимо подсчитать количество подстрок, в которых встречаются все гласные буквы ('a', 'e', 'i', 'o', 'u') хотя бы по одному разу и ровно k согласных.
💡 Идея
Будем использовать подход «скользящего окна», отслеживая позиции последних появлений гласных и согласных букв.
Это позволяет эффективно перемещать границы окна и быстро проверять условия задачи при изменении количества согласных и наличии всех гласных.
🛠️ Детали подхода
- Для каждой гласной буквы сохраняется её последняя позиция.
- Для согласных используется итератор, последовательно предоставляющий позиции согласных в строке.
- Если количество согласных становится больше
k, левая граница окна перемещается вперёд.
- При каждом совпадении условий (ровно
k согласных и присутствуют все гласные) подсчитывается количество допустимых подстрок.
⏳ Асимптотика
Читать дальше →
ответить
Ссылка на задачу — 2379. Minimum Recolors to Get K Consecutive Black Blocks.
📌 Описание задачи
Дана строка blocks, состоящая из символов 'W' (белый) и 'B' (чёрный).
Необходимо определить минимальное число перекрашиваний белых блоков в чёрные, чтобы получить хотя бы одну последовательность из k подряд идущих чёрных блоков.
💡 Идея
Используем технику скользящего окна:
- будем двигать окно размера
k по строке и считать количество белых блоков внутри окна;
- минимальное количество белых блоков среди всех окон и будет ответом.
📖 Детали подхода
- Посчитаем число белых блоков в первом окне размера
k.
- Сдвигаем окно вправо на один символ за раз:
- если символ, который «входит» в окно, белый (
'W'), увеличиваем счётчик;
- если символ, который «выходит» из окна, белый, уменьшаем счётчик.
- После каждого сдвига окна обновляем минимальное найденное значение.
- Итоговый ответ — это минимальное число белых блоков за всё время обхода.
⏳ Асимптотика
- Время:
O(n) — каждый символ просматривается не более двух раз.
- Память:
O(1) — используется константная дополнительная память.
🛠️ Исходный код
impl Solution {
pub fn minimum_recolors(blocks: String, k: i32) -> i32 {
let blocks = blocks.as_bytes();
let k = k as usize;
// Count white blocks ('W') in the first window of size k
let initial_recolors = blocks[..k].iter().filter(|&&b| b == b'W').count() as i32;
// Slide window over the blocks using iterator methods
blocks
.windows(k+1)
.fold((initial_recolors, initial_recolors), |(current, min), window| {
// Update recolors based on outgoing and incoming blocks
let next = current
+ (window.last() == Some(&b'W')) as i32
- (window.first() == Some(&b'W')) as i32;
(next, min.min(next))
}).1
}
}
Tags: #rust #algorithms #counting
ответить
Предположительно, тебя повысили за то, что ты что-то делал руками лучше всех. Ты будешь много где встречать советы вроде "теперь всё изменилось, у тебя другая работа, прекращай работать руками" и т.п. Это может быть верно, но может быть и херней. До тех пор, пока ты можешь лично создавать 30% или больше от артефактов (строчек кода, фичей, смысла), которые требуются от команды, забей на всякую муть типа методологий и пиплменеджмента и просто продолжай. Да, так ты "на самом деле" "не руководитель", а просто мощный волчара, но шансы на успех будут гораздо выше, чем если ты будешь всё делать как в книжке. Дело даже не в том, что ты напишешь кучу кода, а в том, что это будет твой код, ты будешь хорошо понимать, что в нем и вокруг вообще происходит, и что сколько стоит. Когда у тебя в команде будет 50 человек или больше, это тебе очень пригодится.
В какой-то момент тебе захочется, чтобы команда перестала тебя ограничивать. Для этого нужно, чтобы в ней не было идиотов, и чтобы хватало рабочих рук. Поэтому придется этим заняться самому. В твоей компании на эту тему наверняка есть куча странных ритуалов, их, по возможности, нужно обойти, чтобы как можно быстрее выгнать некомпетентных кретинов. Обычно можно научиться делать их работу за них в 10 раз быстрее, тогда можно будет их сначала выгнать, а потом нанять замену, а не наоборот. Нанимать лучше "умных", а не "опытных" (еще лучше и то и другое, но у вас столько денег нет). Сделать из умных опытных легко, а в обратную сторону невозможно, ну или я не умею.
Вновь нанятых нужно научить работать. Единственный способ это сделать это кодревью, местами переходящий в парное программирование (это единственный смысл в парном программировании). В этот момент можно научить нового человека работать втрое быстрее, чем его предшественник. Главное, чтобы он об этом не догадался.
Где-то в этот момент ты обнаружишь, что лично создаешь уже не очень значимую часть финальных артефактов. Это хорошо, ты стал руководителем, только не методом "давайте всё сломаем, потому что так в книжке написано", а естественным образом.
В этот момент надо заставить команду набрать импульс самостоятельно. Чтобы каждый день в проекте происходило что-то ценное, даже если ты за этим не следишь детально.
Типичные примеры такие:
- придумать каждому хорошему человеку задачу на вырост, в рамках которой он, если захочет зажечь, будет заниматься чем-то полезным (иначе он займется рандомом типа "переписать всё на расте")
- научить людей содержательно ревьюить код друг друга, чтобы они не ждали твоего ценного мнения
- научить людей строить системы так, как ты бы сам их строил (то есть простые и работающие)
- (специфично для ML) настроить сбор обучающих данных с максимальной скоростью
Ну вот в принципе и всё, таким способом ты сможешь собрать крутую команду, создавать с ней офигительный хайтек и менять мир к лучшему. Потом повысят все равно не тебя, потому что топ-менеджмент формируется не так, но это уже совсем другая история.
9 ответов
Очередная наша задача — 2579. Count Total Number of Colored Cells, как ни странно, красиво решается на шахматной доске ☺.
📜 Описание задачи
Дана бесконечная двумерная сетка с неокрашенными клетками. В течение n минут выполняются следующие действия:
- В первую минуту любая клетка окрашивается в синий цвет.
- В каждую следующую минуту закрашиваются все неокрашенные клетки, имеющие общую сторону с уже окрашенными.
Необходимо вычислить количество окрашенных клеток после n минут.
🧠 Идея
Если рассмотреть процесс закрашивания клеток на шахматной доске, можно увидеть, что в момент n окрашенные клетки образуют два наложенных квадрата:
- Квадрат размером
n × n
- Квадрат размером
(n-1) × (n-1)
Сумма площадей этих двух квадратов и дает общее количество окрашенных клеток.
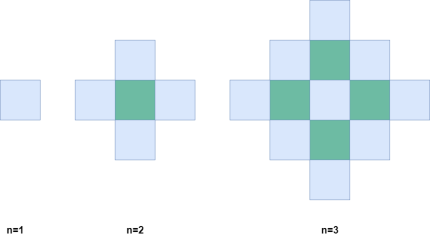
🚀 Детали подхода
✅ Применяем формулу: Total = n²+(n−1)²
⏳ Асимптотика
- Временная сложность:
O(1)
(мгновенный расчет по формуле)
- Пространственная сложность:
O(1)
(используется только переменная n)
💻 Исходный код
impl Solution {
pub fn colored_cells(n: i32) -> i64 {
let n = n as i64;
n*n + (n-1)*(n-1)
}
}
Tags: #rust #algorithms #math
ответить
Ссылка на задачу - 2161. Partition Array According to Given Pivot.
В данной задаче нам предстоит реализовать базовую подзадачу Быстрой сортировки, но с дополнительным требованием сохранения относительного порядка, отчего стандартные методы реализации Q-sort нас не будут устраивать ☹
📌 Описание задачи
Дан массив nums и число pivot. Требуется переставить элементы массива так, чтобы:
- Все элементы меньше
pivot шли первыми.
- Все элементы равные
pivot находились в середине.
- Все элементы больше
pivot шли в конце.
- Относительный порядок элементов в каждой группе сохранялся.
💡 Идея
Мы хотим разделить массив на три части, не создавая лишние структуры данных.
Вместо этого заполним результирующий вектор напрямую, обрабатывая массив в три прохода.
🛠️ Детали подхода
1️⃣ Первый проход: добавляем в результат все элементы < pivot.
2️⃣ Подсчет и второй проход: вычисляем количество вхождений pivot в массиве и добавляем pivot в результат pivot_count раз.
3️⃣ Третий проход: добавляем все элементы > pivot в результат.
Используем Vec::with_capacity(nums.len()), чтобы избежать лишних аллокаций.
📊 Асимптотика
- Временная сложность:
O(n) — три прохода по nums.
- Дополнительная память:
O(1) — все данные хранятся только в результирующем массиве
(который всё же имеет размер O(n)).
💻 Исходный код
impl Solution {
pub fn pivot_array(nums: Vec<i32>, pivot: i32) -> Vec<i32> {
let mut result = Vec::with_capacity(nums.len());
// First pass: Collect elements smaller than pivot
result.extend(nums.iter().filter(|&&num| num < pivot));
// Count occurrences of pivot
let pivot_count = nums.iter().filter(|&&num| num == pivot).count();
// Insert pivot elements
result.extend(std::iter::repeat(pivot).take(pivot_count));
// Third pass: Collect elements greater than pivot using into_iter() to take ownership
result.extend(nums.into_iter().filter(|&num| num > pivot));
result
}
}
Tags: #rust #algorithms
1 ответ
Ссылка на задачу - 1780. Check if Number is a Sum of Powers of Three.
📌 Описание задачи
Дано число n. Нужно определить, можно ли представить его в виде суммы различных степеней тройки.
🔹 Пример:
- 📥 Ввод:
n = 12
- 📤 Вывод:
true
- 💡 Объяснение:
12 = 3⁰+3¹+3² = 1 + 3 + 9.
💡 Идея
Рассмотрим представление n в троичной системе счисления:
- Если в записи числа есть цифра
2, то решения нет (так как нельзя взять две одинаковые степени).
- Если в записи есть только
0 и 1, то решение существует (мы просто берём соответствующие степени тройки).
Таким образом, задача сводится к поразрядной проверке числа в троичной системе счисления.
🚀 Детали подхода
Будем использовать рекурсию и деление числа на 3:
- База рекурсии: Если
n == 0, то мы успешно разложили число, возвращаем true.
- Шаг рекурсии: Если
n % 3 == 2, то n нельзя разложить, возвращаем false.
- Рекурсивный вызов: Проверяем
n / 3, повторяя процесс.
⏱ Асимптотика
- Временная сложность:
O(log n), так как n уменьшается в 3 раза за итерацию.
- Пространственная сложность:
O(log n) из-за глубины рекурсии
(несложно алгоритм преобразовать в цикл, чтобы получить O(1)).
📝 Исходный код
impl Solution {
pub fn check_powers_of_three(n: i32) -> bool {
n == 0 || (n % 3 != 2 && Self::check_powers_of_three(n / 3))
}
}
Tags: #rust #algorithms #math
ответить
Ссылка на задачу - 2570. Merge Two 2D Arrays by Summing Values.
📌 Описание задачи
Даны два отсортированных списка nums1 и nums2, где каждый элемент представлен в виде [id, value].
Нужно объединить их в один список, упорядоченный по id, при этом суммируя значения для совпадающих id.
💡 Идея
Так как оба списка уже отсортированы по id, можно пройтись по ним одновременно, сравнивая id и добавляя элементы в результат.
Такой метод позволяет решить задачу за O(n + m) без дополнительной сортировки.
🛠 Подробности подхода
- Используем два индекса
i и j для итерации по nums1 и nums2.
- Сравниваем текущие
id:
- Если
id1 < id2 → добавляем nums1[i] в результат, сдвигаем i.
- Если
id1 > id2 → добавляем nums2[j] в результат, сдвигаем j.
- Если
id1 == id2 → суммируем значения, добавляем результат, сдвигаем оба указателя.
- Добавляем оставшиеся элементы из
nums1 и nums2, если таковые имеются.
Читать дальше →
ответить
Ссылка на задачу — 2460. Apply Operations to an Array.
📝 Описание задачи
Дан массив nums, состоящий из неотрицательных целых чисел. Нужно последовательно выполнить следующие операции:
- Для каждого валидного
i (в порядке возрастания):
- eсли
nums[i] == nums[i + 1], удвоить nums[i] и заменить nums[i + 1] на 0.
- После всех операций сдвинуть все нули в конец массива, сохраняя порядок оставшихся чисел.
- Вернуть изменённый массив.
💡 Идея
Решение можно выполнить за один проход, используя два указателя (read и write):
- Читаем массив и объединяем соседние одинаковые элементы.
- Перемещаем ненулевые элементы в начало массива.
- Оставшиеся ячейки заполняем нулями.
Такой подход позволяет изменять массив на месте, не используя дополнительную память.
📌 Детали подхода
- Используем два указателя (
read и write):
read проходит по массиву.write отслеживает следующую позицию для ненулевых чисел.
Читать дальше →
ответить
Ссылка на задачу — 873. Length of Longest Fibonacci Subsequence.
📌 Описание задачи
Дан монотонно возрастающий массив arr. Нужно найти длину самой длинной фибоначчиевой подпоследовательности, где каждые три последовательных элемента x, y, z удовлетворяют свойству: z = x + y
Если такой подпоследовательности нет, вернуть 0.
💡 Идея
- Мы используем динамическое программирование для отслеживания самой длинной допустимой фибоначчиевой подпоследовательности для всех нетривиальных пар
(z, y), где:
x,y,z=x+y ∈ arr и x<y<z
- Рекурентное правило ДП:
dp[z,y]=dp[y,x]+1
- Для поиска подходящих
(x, y) к текущему z применяем двунаправленный итератор.
📌 Подробности метода
- Перебираем
z = arr[k], начиная с k = 2, так как нужны минимум 3 числа.
- Будем использовать два указателя (
front и back) на arr[..k]:
front движется вперёд (x увеличивается).back движется назад (y уменьшается).
- Сравниваем
x + y и z:
Читать дальше →
1 ответ
Ссылка на задачу — 1524. Number of Sub-arrays With Odd Sum.
📌 Описание задачи
Дан массив целых чисел arr. Необходимо найти количество подмассивов с нечётной суммой.
Так как ответ может быть очень большим, его необходимо вернуть по модулю 10⁹+7.
💡 Идея
Вместо явного перебора всех подмассивов (O(N²)), можно следить за чётностью суммы префикса.
Ключевое наблюдение:
- Если текущая сумма чётная, то количество новых подмассивов с нечётной суммой равно числу префиксов с нечётной суммой.
- Если текущая сумма нечётная, то число новых подмассивов с нечётной суммой равно количеству префиксов с чётной суммой.
🛠 Детали подхода
- Следим за чётностью префиксной суммы, храня в
prefix_parity (0 - чётная, 1 - нечётная).
- Считаем количество чётных (
even_count) и нечётных (odd_count) префиксных сумм.
- Используем
fold для итеративного обновления результата.
- Добавляем соответствующие значения к result:
- Если
prefix_parity чётный, к result прибавляем odd_count.
- Если
prefix_parity нечётный, к result прибавляем even_count.
⏳ Асимптотика
- Время:
O(N) — один проход по массиву.
- Память:
O(1) — используем только несколько переменных.
💻 Исходный код
impl Solution {
pub fn num_of_subarrays(arr: Vec<i32>) -> i32 {
const MODULO: i32 = 1_000_000_007;
let (result, _, _, _) = arr.into_iter()
.fold((0, 0, 0, 1), |(result, prefix_parity, odd_count, even_count), num| {
match(prefix_parity + num) % 2 {
0 => // Even prefix → account subarrays from odd prefixes
((result + odd_count) % MODULO, 0, odd_count, even_count + 1),
_ => // Odd prefix → account subarrays from even prefixes
((result + even_count) % MODULO, 1, odd_count + 1, even_count),
}
});
result
}
}
Tags: #rust #algorithms #prefixsum
ответить
Ссылка на задачу — 2467. Most Profitable Path in a Tree.
📌 Описание задачи
Дано неориентированное корневое дерево с n узлами (нумерованными от 0 до n-1).
- У каждого узла есть врата, открытие которых может принести прибыль или потребовать затрат (
amount[i]).
- Алиса начинает движение от корня (
0) к какому-либо листу, выбирая максимально выгодный путь.
- Боб начинает движение из указанной вершины
bob и движется к корню (0).
- Если Алиса и Боб одновременно посещают узел, они делят
стоимость/прибыль пополам.
Нужно найти максимальный чистый доход Алисы при оптимальном выборе пути.
💭 Идея
Вместо раздельного запуска BFS для поиска пути Боба и последующего прохода динамического программирования по узлам дерева, мы решим задачу одним рекурсивным DFS-проходом.
Для каждого узла будем вычислять:
alice_profit[node] – максимальный доход, который может собрать Алиса из поддерева.bob_distance[node] – расстояние на пути Боба до этой вершины.- Если Боб раньше доберётся до узла → Алиса ничего не получит.
Читать дальше →
ответить
Ссылка на задачу — 889. Construct Binary Tree from Preorder and Postorder Traversal.
📌 Описание задачи
Нам даны прямой (preorder) и обратный (postorder) обходы бинарного дерева.
Необходимо восстановить дерево по этим обходам.
Основные свойства обходов:
- Preorder (прямой обход):
[корень → левый → правый]
- Postorder (обратный обход):
[левый → правый → корень]
💡 Идея
Для построения дерева используем рекурсивный подход, основанный на двух ключевых наблюдениях:
- 1️⃣ Каждый новый узел получает значение из
preorder
→ так мы всегда сначала создаем корень поддерева.
- 2️⃣ Поддерево считается полностью построенным, когда его значение встречается в
postorder
→ это сигнал к завершению рекурсии.
🔍 Детали подхода
- Используем итераторы
Peekable<Iterator> для эффективного прохода по preorder и postorder.
- Берем значение из
preorder и создаем новый узел.
- Рекурсивно создаем левое поддерево, если
postorder пока не указывает на текущий корень.
Читать дальше →
ответить
Ссылка на задачу — 1028. Recover a Tree From Preorder Traversal.
📝 Описание задачи
Дано строковое представление бинарного дерева, полученное в порядке прямого обхода, где:
- Каждый узел записан в формате
Dashes + Value, где количество - (тире) указывает на глубину узла.
- Глубина корневого узла —
0, его дочерний узел имеет глубину 1, внуки — 2 и так далее.
- Если у узла есть только один ребёнок, то это всегда левый ребёнок.
Например для следующего дерева, представление будет таким: 1-2--3---4-5--6---7
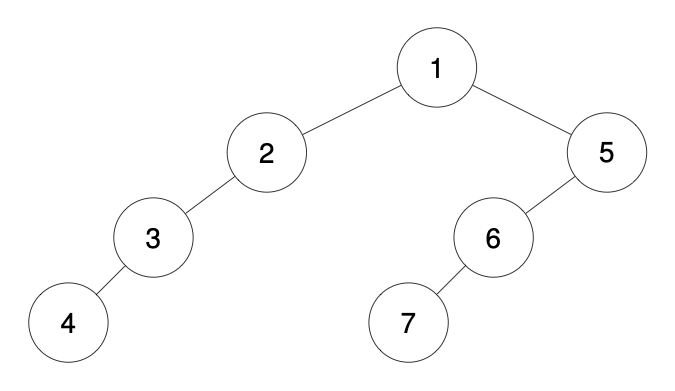
Необходимо восстановить бинарное дерево по этой строке и вернуть его корень.
💡 Идея
- Нам нужно восстановить бинарное дерево из его обхода с закодированными глубинами.
- Традиционное решение:
- разбить строку на токены (
Dashes + Value);
- затем рекурсивно собрать дерево по массиву токенов.
- Мы же сделаем чуть больше работы, и будем лениво разбирать представление на токены (вместо того, чтобы сразу сохранить их в
Vec)
Читать дальше →
ответить
Ссылка на задачу – 1261. Find Elements in a Contaminated Binary Tree.
📝 Описание задачи
Дано двоичное дерево, в котором:
- Корень всегда имеет значение
0.
- Для каждого узла со значением
x:
- Если есть левый потомок, то его значение
2 * x + 1.
- Если есть правый потомок, то его значение
2 * x + 2.
Значения всех узлов загрязнены (-1).
Нужно реализовать структуру FindElements, которая:
- Принимает корень «загрязнённого» дерева в конструкторе.
- Реализует
find(target) — метод, проверяющий существует ли узел с таким значением.
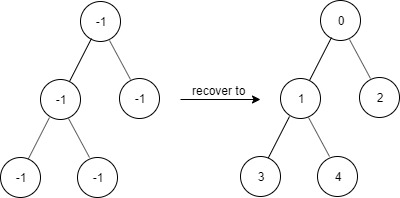
💡 Идея
Восстанавливать дерево не требуется!
Вместо этого мы вычисляем путь к узлу target, определяя его родителя и положение.
🔍 Детали подхода
- Поиск родителя (
parent):
Читать дальше →
ответить
Ссылка на задачу — 1980. Find Unique Binary String.
Кайфовая задачка для тех, кто не прогуливал лекции по мат. анализу ☺
📌 Описание задачи
Дан массив nums, содержащий n различных бинарных строк длины n.
Необходимо найти любую бинарную строку длины n, которая не содержится в nums.
💡 Идея
Используем диагонализацию Кантора:
- Если пройти по диагонали массива строк и инвертировать каждый символ (
'0' → '1', '1' → '0'), то полученная строка гарантированно отличается от каждой строки в nums хотя бы в одном символе.
- Это означает, что такая строка не может присутствовать в
nums.
🔍 Подробности подхода
- Итерируемся по индексам
0..n.
- Берем
i-й символ i-й строки.
- Инвертируем его (
'0' → '1', '1' → '0').
- Собираем новые символы в строку и возвращаем её.
📊 Асимптотика
- Временная сложность:
O(n) — один проход по n элементам.
- Дополнительная память:
O(n) — единственное, что создаётся, это строка длины n.
Визуальный пример
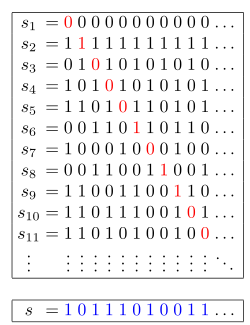
🦀 Исходный код
impl Solution {
pub fn find_different_binary_string(nums: Vec<String>) -> String {
let n = nums.len();
// Generate a new binary string by flipping the diagonal elements.
(0..n)
.map(|i| Self::inverse_char(nums[i].as_bytes()[i] as char))
.collect()
}
fn inverse_char(c: char) -> char {
match c {
'0' => '1',
'1' => '0',
_ => unreachable!("Unexpected character: {}", c),
}
}
}
Tags: #rust #algorithms #math
ответить
Страница
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
