Ссылка на задачу – 1261. Find Elements in a Contaminated Binary Tree.
📝 Описание задачи
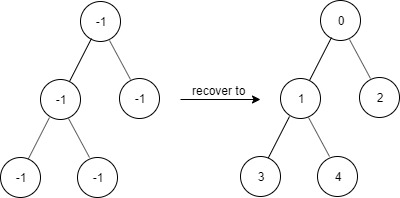
Дано двоичное дерево, в котором:
- Корень всегда имеет значение
0.
- Для каждого узла со значением
x:
- Если есть левый потомок, то его значение
2 * x + 1.
- Если есть правый потомок, то его значение
2 * x + 2.
Значения всех узлов загрязнены (-1).
Нужно реализовать структуру FindElements, которая:
- Принимает корень «загрязнённого» дерева в конструкторе.
- Реализует
find(target) — метод, проверяющий существует ли узел с таким значением.
💡 Идея
Восстанавливать дерево не требуется!
Вместо этого мы вычисляем путь к узлу target, определяя его родителя и положение.
🔍 Детали подхода
-
Поиск родителя (
parent):
- Если target == 0, значит это корень, возвращаем Some(root).
- Иначе вычисляем значение родителя:
parent_val = (target - 1) / 2.
- Рекурсивно находим узел
parent.
-
Определение левого/правого потомка:
- Если
parent не найден, значит target тоже не существует.
- Если
(target - 1) % 2 == 0, то возвращаем parent.left.
- Иначе —
parent.right.
-
Финальная проверка:
- Если
find_recursive вернул Some(_), значит узел существует.
📊 Асимптотика
-
Время работы:
O(log target)
- Мы делим
target на 2 на каждом уровне рекурсии → глубина = log(target).
-
Память:
O(log target)
- Использование стека определяется глубиной рекурсии —
log(target)
📝 Исходный код
use std::rc::Rc;
use std::cell::RefCell;
// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
struct FindElements {
root: Option<Rc<RefCell<TreeNode>>>
}
impl FindElements {
fn new(root: Option<Rc<RefCell<TreeNode>>>) -> Self {
FindElements { root }
}
// Checks if the target value exists in the tree
pub fn find(&self, target: i32) -> bool {
find_recursive(self.root.clone(), target).is_some()
}
}
// Recursively finds the target node by first locating its parent
fn find_recursive(node: Option<Rc<RefCell<TreeNode>>>, target: i32) -> Option<Rc<RefCell<TreeNode>>> {
if target == 0 {
return node; // Base case: root is always at value 0
}
let parent_val = (target - 1) / 2;
match (target - 1) % 2 {
0 => find_recursive(node, parent_val)?.borrow().left.clone(),
1 => find_recursive(node, parent_val)?.borrow().right.clone(),
_ => unreachable!("unexpected mod 2 value")
}
}
Tags: #rust #algorithms #tree