Ссылка на задачу — 1028. Recover a Tree From Preorder Traversal.
📝 Описание задачи
Дано строковое представление бинарного дерева, полученное в порядке прямого обхода, где:
- Каждый узел записан в формате
Dashes + Value, где количество - (тире) указывает на глубину узла.
- Глубина корневого узла —
0, его дочерний узел имеет глубину 1, внуки — 2 и так далее.
- Если у узла есть только один ребёнок, то это всегда левый ребёнок.
Например для следующего дерева, представление будет таким: 1-2--3---4-5--6---7
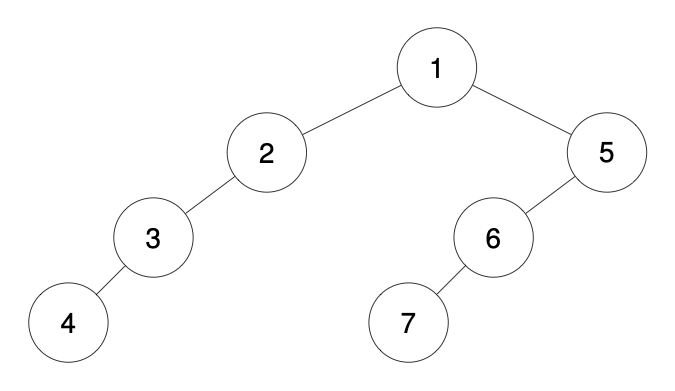
Необходимо восстановить бинарное дерево по этой строке и вернуть его корень.
💡 Идея
- Нам нужно восстановить бинарное дерево из его обхода с закодированными глубинами.
- Традиционное решение:
- разбить строку на токены (
Dashes + Value);
- затем рекурсивно собрать дерево по массиву токенов.
- Мы же сделаем чуть больше работы, и будем лениво разбирать представление на токены (вместо того, чтобы сразу сохранить их в
Vec)
- Будем пользоваться
Peekable итераторами, которые обеспечивают нам предпросмотр за константное время.
🛠 Детали метода
-
Ленивый парсинг токенов:
- Реализуем
Tokenizer, который реализует интерфейс итератора по токенам.
- Каждый вызов
next() считывает один узел (глубина + значение) из строки на лету.
-
Строительство дерева:
- Используем
Peekable<Tokenizer> для эффективного заглядывания вперед (peek()), не съедая токен.
- Если следующий узел на меньшей глубине, то останавливаемся и возвращаем
None.
- Иначе создаем узел и рекурсивно строим его левое и правое поддерево.
⏳ Асимптотика
- Время:
O(n), так как каждый символ строки обрабатывается ровно один раз.
- Память:
O(h), где h — глубина дерева (O(log n) для сбалансированного, O(n) для вырожденного).
💻 Исходный код
use std::rc::Rc;
use std::cell::RefCell;
use std::iter::Peekable;
use std::str::Chars;
// Structure of the TreeNode
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
struct Tokenizer<'a> {
chars: Peekable<Chars<'a>>,
}
impl Solution {
pub fn recover_from_preorder(traversal: String) -> Option<Rc<RefCell<TreeNode>>> {
let tokenizer = Tokenizer::new(&traversal);
let mut tokens = tokenizer.peekable();
Self::build_tree(0, &mut tokens)
}
// Recursively builds the tree using a generic Peekable iterator
fn build_tree<T>(depth: usize, tokens: &mut Peekable<T>) -> Option<Rc<RefCell<TreeNode>>>
where
T: Iterator<Item = (usize, i32)>,
{
// Stop if there are no more nodes or the next node is at a shallower depth
if tokens.peek().map_or(true, |&(d, _)| d < depth) {
return None;
}
let (_, val) = tokens.next().unwrap(); // Safe because we checked peek()
let node = Rc::new(RefCell::new(TreeNode { val, left: None, right: None }));
// Recursively assign left and right children if they exist
if tokens.peek().map_or(false, |&(d, _)| d == depth + 1) {
node.borrow_mut().left = Self::build_tree(depth + 1, tokens);
}
if tokens.peek().map_or(false, |&(d, _)| d == depth + 1) {
node.borrow_mut().right = Self::build_tree(depth + 1, tokens);
}
Some(node)
}
}
impl<'a> Tokenizer<'a> {
fn new(traversal: &'a str) -> Self {
Self { chars: traversal.chars().peekable() }
}
// Parses depth (number of '-')
fn parse_depth(&mut self) -> usize {
let mut depth = 0;
while self.chars.peek() == Some(&'-') {
self.chars.next();
depth += 1;
}
depth
}
// Parses the numeric value of a node
fn parse_value(&mut self) -> i32 {
let mut num = 0;
while let Some(&ch) = self.chars.peek() {
if let Some(digit) = ch.to_digit(10) {
num = num * 10 + digit as i32;
self.chars.next();
} else {
break;
}
}
num
}
}
impl<'a> Iterator for Tokenizer<'a> {
type Item = (usize, i32);
fn next(&mut self) -> Option<Self::Item> {
let depth = self.parse_depth();
if self.chars.peek().is_none() {
return None;
}
let value = self.parse_value();
Some((depth, value))
}
}
Tags: #rust #algoriths #parser #tree