Задача 7-го дня Advent of Code — Bridge Repair.
📘 Часть I. Условие задачи
У инженеров почти готова калибровка оборудования, но из формул пропали все операторы!
Остались только числа. В каждой строке входных данных указано:
- Слева — целевое значение;
- Справа — последовательность чисел.
Задача: вставить между числами операторы + и *, чтобы получить целевое значение.
Важно: выражения вычисляются строго слева направо, без учёта приоритетов операций.
Например:
190: 10 19
3267: 81 40 27
Требуется определить, какие строки могут быть истинными, и посчитать сумму их целевых значений.
💡 Идея
- Каждую строку можно представить как выражение, в которое надо вставить операторы.
- Количество вставок —
len(seq) - 1.
- Для каждой строки мы перебираем все возможные комбинации из операторов
+ и * и проверяем, приводит ли результат к целевому числу.
Так как порядок чисел менять нельзя и вычисления всегда происходят слева направо, задача хорошо ложится на рекурсивный перебор (бэктрекинг).
Читать дальше →
ответить
Очередная наша задача — 2579. Count Total Number of Colored Cells, как ни странно, красиво решается на шахматной доске ☺.
📜 Описание задачи
Дана бесконечная двумерная сетка с неокрашенными клетками. В течение n минут выполняются следующие действия:
- В первую минуту любая клетка окрашивается в синий цвет.
- В каждую следующую минуту закрашиваются все неокрашенные клетки, имеющие общую сторону с уже окрашенными.
Необходимо вычислить количество окрашенных клеток после n минут.
🧠 Идея
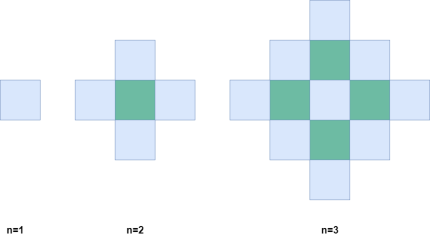
Если рассмотреть процесс закрашивания клеток на шахматной доске, можно увидеть, что в момент n окрашенные клетки образуют два наложенных квадрата:
- Квадрат размером
n × n
- Квадрат размером
(n-1) × (n-1)
Сумма площадей этих двух квадратов и дает общее количество окрашенных клеток.
🚀 Детали подхода
✅ Применяем формулу: Total = n²+(n−1)²
⏳ Асимптотика
- Временная сложность:
O(1)
(мгновенный расчет по формуле)
- Пространственная сложность:
O(1)
(используется только переменная n)
💻 Исходный код
impl Solution {
pub fn colored_cells(n: i32) -> i64 {
let n = n as i64;
n*n + (n-1)*(n-1)
}
}
Tags: #rust #algorithms #math
ответить
Ссылка на задачу - 1780. Check if Number is a Sum of Powers of Three.
📌 Описание задачи
Дано число n. Нужно определить, можно ли представить его в виде суммы различных степеней тройки.
🔹 Пример:
- 📥 Ввод:
n = 12
- 📤 Вывод:
true
- 💡 Объяснение:
12 = 3⁰+3¹+3² = 1 + 3 + 9.
💡 Идея
Рассмотрим представление n в троичной системе счисления:
- Если в записи числа есть цифра
2, то решения нет (так как нельзя взять две одинаковые степени).
- Если в записи есть только
0 и 1, то решение существует (мы просто берём соответствующие степени тройки).
Таким образом, задача сводится к поразрядной проверке числа в троичной системе счисления.
🚀 Детали подхода
Будем использовать рекурсию и деление числа на 3:
- База рекурсии: Если
n == 0, то мы успешно разложили число, возвращаем true.
- Шаг рекурсии: Если
n % 3 == 2, то n нельзя разложить, возвращаем false.
- Рекурсивный вызов: Проверяем
n / 3, повторяя процесс.
⏱ Асимптотика
- Временная сложность:
O(log n), так как n уменьшается в 3 раза за итерацию.
- Пространственная сложность:
O(log n) из-за глубины рекурсии
(несложно алгоритм преобразовать в цикл, чтобы получить O(1)).
📝 Исходный код
impl Solution {
pub fn check_powers_of_three(n: i32) -> bool {
n == 0 || (n % 3 != 2 && Self::check_powers_of_three(n / 3))
}
}
Tags: #rust #algorithms #math
ответить
Ссылка на задачу — 1980. Find Unique Binary String.
Кайфовая задачка для тех, кто не прогуливал лекции по мат. анализу ☺
📌 Описание задачи
Дан массив nums, содержащий n различных бинарных строк длины n.
Необходимо найти любую бинарную строку длины n, которая не содержится в nums.
💡 Идея
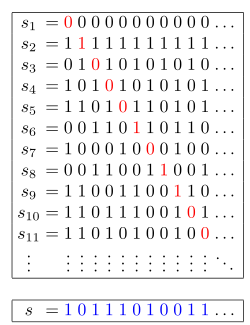
Используем диагонализацию Кантора:
- Если пройти по диагонали массива строк и инвертировать каждый символ (
'0' → '1', '1' → '0'), то полученная строка гарантированно отличается от каждой строки в nums хотя бы в одном символе.
- Это означает, что такая строка не может присутствовать в
nums.
🔍 Подробности подхода
- Итерируемся по индексам
0..n.
- Берем
i-й символ i-й строки.
- Инвертируем его (
'0' → '1', '1' → '0').
- Собираем новые символы в строку и возвращаем её.
📊 Асимптотика
- Временная сложность:
O(n) — один проход по n элементам.
- Дополнительная память:
O(n) — единственное, что создаётся, это строка длины n.
Визуальный пример
🦀 Исходный код
impl Solution {
pub fn find_different_binary_string(nums: Vec<String>) -> String {
let n = nums.len();
// Generate a new binary string by flipping the diagonal elements.
(0..n)
.map(|i| Self::inverse_char(nums[i].as_bytes()[i] as char))
.collect()
}
fn inverse_char(c: char) -> char {
match c {
'0' => '1',
'1' => '0',
_ => unreachable!("Unexpected character: {}", c),
}
}
}
Tags: #rust #algorithms #math
ответить
Ссылка на задачу – 2364. Count Number of Bad Pairs.
📌 Описание задачи
Дан массив nums, где пара индексов (i, j) называется плохой, если выполняется:
Требуется найти общее количество таких плохих пар.
💡 Идея
- Запишем условие хорошей пары:
j−i = nums[j]−nums[i]
- Переставляя слагаемые, получаем:
nums[j]−j = nums[i]−i
То есть если два индекса имеют одинаковое значение позиционной разности (nums[k] - k), – они образуют хорошую пару!
🛠️ Детали метода
- Создаём массив позиционных разностей:
pos_diff[i]=nums[i]−i
- Сортируем массив
pos_diff, группируя одинаковые значения.
- Используем метод
chunk_by для подсчёта частот одинаковых значений.
- Для каждой такой частоты
count, вычисляем количество хороших пар:
count×(count−1)/2
- Всего существует
n × (n - 1) / 2 пар, из них вычитаем хорошие пары и получаем ответ.
⏳ Асимптотика
- Время:
O(n·log n), так как сортировка доминирует над остальными операциями.
- Память:
O(n), так как храним pos_diff.
🔥 Хотя сортировка для подсчёта частот медленнее хеш-таблиц в асимптотике, на практике она быстрее из-за низкой константы!
📝 Исходный код
impl Solution {
pub fn count_bad_pairs(nums: Vec<i32>) -> i64 {
let n = nums.len() as i64;
// Compute adjusted values (nums[i] - i) and sort
let mut pos_diff: Vec<_> = nums.into_iter()
.enumerate()
.map(|(idx, num)| num - idx as i32)
.collect();
pos_diff.sort_unstable();
// Count good pairs using `chunk_by`
let good_pairs: i64 = pos_diff
.chunk_by(|a, b| a == b)
.map(|chunk| (chunk.len() as i64 * (chunk.len() as i64 - 1)) / 2)
.sum();
// Total pairs - good pairs = bad pairs
let total_pairs = n * (n - 1) / 2;
total_pairs - good_pairs
}
}
Tags: #rust #algorithms #math
ответить
Ссылка на задачу — 2523. Closest Prime Numbers in Range.
📌 Описание задачи
Нам даны два целых числа left и right.
Нужно найти два ближайших простых числа num1 и num2 таких, что:
left ≤ num1 < num2 ≤ right- Оба числа простые
- Разница
num2 - num1 минимальна среди всех возможных пар
Если существует несколько пар с одинаковой разницей, выбрать пару с меньшим первым числом.
Если таких чисел нет, вернуть [-1, -1].
🧠 Идея
Будем просто итерироваться по парам соседних простых чисел в заданом диапазоне.
Но, так как простые близнецы (пары простых чисел, разница между которыми равна 2) встречаются довольно часто (их плотность примерно 1 / log²(n)) мы можем эффективно ввести условие раннего выхода, которое значительно улучшает среднюю производительность алгоритма.
🔍 Подход
- Обработка граничных случаев:
- Если
left ≤ 2 и right ≥ 3, сразу возвращаем [2, 3].
- Перебор чисел в диапазоне:
- Проверяем каждое число на простоту с помощью
is_prime(n), работающей за O(√n).
Читать дальше →
ответить
Ссылка на задачу — 2965. Find Missing and Repeated Values.
📌 Описание задачи
Дан n×n целочисленный массив grid, содержащий числа от 1 до n².
Одно число повторяется дважды (a), а одно отсутствует (b).
Нужно найти их.
💡 Идея
Мы можем использовать математические свойства сумм чисел:
Разница между ожидаемыми и фактическими значениями позволит выразить a и b через систему уравнений.
🚀 Детали подхода
- Вычисляем ожидаемую сумму и ожидаемую сумму квадратов для чисел от
1 до n².
- Проходим по
grid, вычисляя фактическую сумму и фактическую сумму квадратов.
- Находим промежуточные величины для системы уравнений:
Читать дальше →
ответить
Был у меня был период увлечения математической логикой в тщетной попытке понять доказательство независимости континуум-гипотезы от ZFC. Хочу рассказать оттуда об одном занимательном факте и предложить не очень сложную, но красивую, на мой взгляд, задачку.
Сначала немного определений. Назовём структурой произвольное множество M, на котором заданы какие-то отношения. Например, (N, <) - множество натуральных чисел с отношением "меньше", или (R, +) - множество действительных чисел с отношением сложения. "Отношение сложения" - это множество всех троек (x, y, z), для которых x + y = z.
Имея структуру, можно задаться вопросом, какие множества в ней определяемы с помощью стандартных логических формул (и, или, отрицание, существует, для любого). Разрешён знак =, который означает совпадение элементов.
Чтобы определить множество, нужно написать формулу с одной свободной переменной, которая будет верна только на этом множестве. Например, множество чётных чисел в структуре (Z, +) определяется формулой "существует y такое, что x = y + y". Свободная переменная здесь - x, и утверждение верно тогда и только тогда, когда x чётное.
Ещё несколько примеров.
-
Ноль в структуре ( Z, +) определяется формулой "x + x = x".
-
Отношение порядка в структуре ( N, +) определяется формулой "существует z такое, что x + z = y". Эта формула верна, когда x < y.
-
Множество неотрицательных чисел в структуре ( Z, +, *) можно определить с помощью теоремы Лагранжа: "cуществуют такие k, l, m, n, что x = k*k + l*l + m*m + n*n".
Читать дальше →
6 ответов
Наверняка у вас были книжки о математике/программированию, которыми вы зачитывались в подростковом возрасте?
Из тех, которые запомнились мне:
"Математические новеллы", Гарднера и "Алиса в стране смекалки" Рэймонда Смаллиана - обе могу порекомендовать как взрослым, так и детям. #books #math
4 ответа
Все, кто занимается анализом данных, статистикой, машинным обучением или похожими дисциплинами, слышали поговорку "correlation doesn't imply causation" ("наличие корреляции не означает наличия причинно-следственной связи"). Сама по себе эта поговорка абсолютно верна, но её легко понять слишком расширительно и сильно навредить тем самым самому себе. А именно, можно решить, что данные в принципе не могут быть основой ни для каких суждений о причинно-следственных связях, и что любой вывод, сделанный на основе той или иной статистики, сам по себе не может быть поводом для каких-либо действий, за исключением "посмотреть сюда внимательнее".
Это, конечно, не так. Если завоняло серой, это не значит, что рядом бродит чёрт, но если завоняло серой, рядом бродит чёрт, а ваш собеседник продолжает отрицать причинно-следственную связь, то, скорее всего, у него просто KPI привязан к тому, чтобы связи не было.
В дискуссии упоминание "correlation doesn't imply causation", соответственно, часто означает "мне не нравятся ваши выводы, поэтому я хочу вас заткнуть". Поинтересуйтесь у такого оппонента, что он думает про двойное слепое рандомизированное тестирование лекарств, обычно восторг от этой практики как-то необъяснимо уживается в одной голове с этой поговоркой.
in#math
5 ответов
Вот, например, международные математические олимпиады : https://www.youtube.com/playlist?list=PL22w63XsKjqycsMoTIRjPhWXTD6F3LslO
Зовут Майкл Пенн, контента много, снято хорошо, очень аддиктивно.
В процессе просмотра его видео перед сном я наконец-то всей душой поверил в несколько вещей, которые головой в принципе знал и до этого:
- математические олимпиады - это такой спорт, типа бега или CodeForces; золото на межнаре это очень крутое достижение, но кроме таланта для этого обязательно нужно быть "в системе" и посвящать подготовке много времени (ну если вы не Терри Тао), а польза от такой гонки довольно сомнительная
- в любой стране есть выдающиеся умы. Опять же, одно дело знать это умом, другое решать вполне содержательные задачки из национальной олимпиады Таджикистана или Нигерии, мало чем отличающиеся от аналогичных из Австрии или Японии, буквально
- при этом ММО (последний уровень) радикально круче национальных олимпиад, мало того, что гробы, но еще и очень неожиданные, ни на что не похожие. Откуда они их берут в таких количествах?
in #youtube, #math
ответить
TLDR: бруски (примерно как в учебнике физики за 7 класс) выдают последовательные знаки числа Пи (естественно, в теории, то есть без трения, в вакууме и все такое). У этого есть красивое объяснение через фазовое пространство.
in#youtube,#math
1 ответ
Серия естественно выглядящих интегралов, каждый из которых равен пи, пока в какой-то момент вдруг не оказывается чем-то типа 0.9999965 пи. При этом не просто рандомный курьёз, а имеет довольно глубокое объяснение через вейвлеты и преобразование Фурье. У меня только в этот момент окончательно кликнуло, зачем эти вейвлеты вообще нужны.
Если есть фантомные боли по поводу того, что вы не стали математиком, рекомендую подписаться на автора, видео он выкладывает нечасто, но общий уровень очень высокий
in#youtube,#math
ответить
