▲

3

▼

🔗 Оптимальный поиск минимальной AND-стоимости пути

leetcoder, 20-03-2025 , 157

Ссылка на задачу — 3108. Minimum Cost Walk in Weighted Graph.

📌 Описание задачи

• Дан неориентированный взвешенный граф с n вершинами и m рёбрами.
• Каждое ребро представлено тройкой [u, v, w], означающей, что существует ребро между u и v с весом w.
• Определим стоимость пути между двумя вершинами как битовое AND всех рёбер, пройденных на пути (вершинам в таком пути разрешено повторяться).
• Для каждого запроса [s, t] требуется найти минимальную AND-стоимость пути между s и t.
• Если пути не существует, ответ -1.

Пример

• Входные данные: n = 5; edges = [[0,1,7],[1,3,7],[1,2,1]]; query = [[0,3],[3,4]]
• Результаты: [1, -1]
• Объяснение:
  • Наилучший путь от 0 до 3: 0 → 1 → 2 → 1 → 3.
  • Путей из 3 в 4 не существует.
• Графическая интерпретация:
  

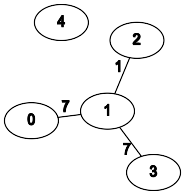
💡 Идея

• Так как каждое новое ребро пути его стоимость не увеличивает, то внутри каждой компоненты связности стоимость минимального пути будет одинаковой (достаточно определить путь, проходящий через все рёбра компоненты связности).
• Таким образом, вместо поиска конкретного пути между s и t, можно разделить граф на компоненты и запомнить минимальный AND среди всех рёбер в каждой компоненте.
• После этого любой запрос [s, t] можно обработать за O(1), просто проверив, находятся ли s и t в одной компоненте.

🚀 Детали подхода

1. Построение графа в виде списка смежности graph.
2. Поиск компонент связности с использованием обхода в глубину (DFS):
   • Каждой компоненте присваивается уникальный идентификатор.
   • Одновременно вычисляется минимальный AND среди всех рёбер в компоненте.
3. Обработка запросов:
   • Если s и t принадлежат разным компонентам, ответ -1.
   • Если s и t принадлежат одной компоненте, ответ — минимальный AND этой компоненты.

⏳ Асимптотика

• Временная сложность: O(N + M + Q)
  • Построение графа (заполнение списка смежности) — O(M)
  • Поиск компонент связности (DFS) — O(N + M)
  • Обработка запросов — O(Q)
• Пространственная сложность: O(N + M)
  • Для хранения графа и массивов компонент

📝 Исходный код

impl Solution {
    pub fn minimum_cost(n: i32, edges: Vec<Vec<i32>>, queries: Vec<Vec<i32>>) -> Vec<i32> {
        let n = n as usize;
        let mut graph = vec![Vec::new(); n];
        let mut component_id = vec![-1; n];

        // Build adjacency list
        for edge in edges {
            let (u, v, w) = (edge[0] as usize, edge[1] as usize, edge[2]);
            graph[u].push((v, w));
            graph[v].push((u, w));
        }

        let mut component_min_and = Vec::new();

        // Identify components and compute min AND for each
        for i in 0..n {
            if component_id[i] == -1 {
                component_min_and.push(Self::dfs(i, &graph, component_min_and.len() as i32, &mut component_id));
            }
        }

        // Process queries
        queries.into_iter()
            .map(|q| {
                let (s, t) = (component_id[q[0] as usize], component_id[q[1] as usize]);
                if s != t { -1 } else { component_min_and[s as usize] }
            }).collect()
    }

    /// Performs DFS to assign a component ID and compute the minimum bitwise AND in the component.
    fn dfs(start: usize, graph: &[Vec<(usize, i32)>], id: i32, component_id: &mut [i32]) -> i32 {
        let mut min_and = -1; // Tracks the minimum AND value in the component
        let mut stack = vec![start];

        while let Some(node) = stack.pop() {
            component_id[node] = id; // Mark node as part of this component

            for &(neighbor, weight) in &graph[node] {
                if component_id[neighbor] == -1 {
                    stack.push(neighbor); // Visit unvisited neighbors
                }
                min_and &= weight; // Update minimum AND value
            }
        }

        min_and
    }
}

Tags: #rust #algorithms #dfs #graph