Ссылка на задачу — 3394. Check if Grid can be Cut into Sections.
📌 Описание задачи
Дано квадратное поле n×n, в котором размещены непересекающиеся прямоугольники.
Необходимо определить, можно ли сделать две горизонтальные или две вертикальные разрезки, чтобы:
- В каждой из трёх частей оказалось хотя бы по одному прямоугольнику.
- Каждый прямоугольник остался ровно в одной части.
Если такие разрезки возможны, вернуть true, иначе — false.
Пример
- Входные данные:
n = 5, rectangles = [[1,0,5,2],[0,2,2,4],[3,2,5,3],[0,4,4,5]]
- Ответ:
true
- Визуальное пояснение:
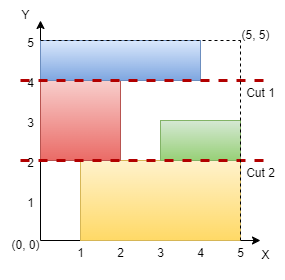
💡 Идея
Поскольку прямоугольники не пересекаются, возможные разрезки должны полностью разделять их на независимые группы.
Мы спроектируем прямоугольники на каждую ось. Если полученные отрезки отсортировать по координатам и просканировать их, можно определить количество неперекрывающихся сегментов, это позволит понять, возможно ли корректное разбиение.
🔍 Детали подхода
- Сортируем прямоугольники по
x-координате начала (start_x).
- Сканируем их, отслеживая количество неперекрывающихся отрезков.
- Повторяем процесс для
y-координаты (start_y), чтобы определить возможные горизонтальные разрезки.
- Если нашлись хотя бы 2 вертикальные или 2 горизонтальные разрезки, возвращаем
true.
⏳ Асимптотика
- Временная сложность:
O(k·log k).
- Сортировка:
O(k·log k), где k — количество прямоугольников.
- Один проход по данным:
O(k).
- Дополнительная память:
O(1) (все операции выполняются на месте).
📝 Исходный код
impl Solution {
pub fn check_valid_cuts(n: i32, mut rectangles: Vec<Vec<i32>>) -> bool {
let vertical_splits = Self::count_possible_splits(&mut rectangles, 0, 0, 2);
let horizontal_splits = Self::count_possible_splits(&mut rectangles, 1, 1, 3);
vertical_splits >= 2 || horizontal_splits >= 2
}
/// Counts the number of non-overlapping segments along a given axis.
fn count_possible_splits(rectangles: &mut [Vec<i32>], sort_index: usize, start_idx: usize, end_idx: usize) -> i32 {
rectangles.sort_unstable_by_key(|r| r[sort_index]);
rectangles.iter()
.map(|rect| (rect[start_idx], rect[end_idx]))
.fold((-1, 0), |(splits, max_end), (start, end)| {
let can_split = start >= max_end;
(splits + can_split as i32, max_end.max(end))
}).0
}
}
Tags: #rust #algorithms #linesweep