Очередная задача — 2375. Construct Smallest Number From DI String сходу выглядит переборной, но может быть эффективно реализована за счёт использования графовых алгоритмов.
📝 Описание задачи
Дан строковый шаблон pattern, состоящий из символов I и D.
Необходимо построить лексикографически наименьшее число длины n+1, используя цифры от 1 до 9 без повторений, которое соответствует следующим требованиям:
'I' (увеличение) на позиции i → требует, чтобы num[i] < num[i+1].'D' (уменьшение) на позиции i → требует, чтобы num[i] > num[i+1].
💡 Идея
Рассмотрим шаблон как ориентированный граф, где каждая позиция (i) — это вершина.
- Если
pattern[i] == 'I', создаём ребро i → i+1.
- Если
pattern[i] == 'D', создаём ребро i+1 → i.
После построения графа можно выполнить топологическую сортировку, начиная с вершин с нулевой степенью захода.
Чтобы гарантировать лексикографически наименьший порядок, обрабатываем вершины через приоритетную очередь (Min-Heap).
⚙️ Детали подхода
Читать дальше →
ответить
Продолжаем череду задач на перебор - 1079. Letter Tile Possibilities.
📜 Описание задачи
У нас есть набор плиток, на каждой из которых напечатана одна буква, представленный в виде строки.
Необходимо подсчитать количество различных возможных непустых последовательностей букв, которые можно составить, используя плитки.
💡 Идея решения
- Будем использовать бэктрекинг.
- Чтобы избежать проверки на уникальность через
HashSet, сначала сортируем плитки, а затем группируем одинаковые плитки в сегменты.
- Далее, с помощью рекурсии, перебираем все возможные последовательности, гарантируя, что одинаковые плитки не будут использоваться более одного раза в одном наборе последовательностей.
🧑💻 Подробности подхода
- Сортировка плиток:
- Плитки сортируются для того, чтобы одинаковые плитки оказались рядом. Это позволяет нам эффективно группировать их в сегменты.
- Группировка плиток:
- Создаем массив сегментов, где каждый элемент представляет собой количество одинаковых плиток.
- Например, для строки
"AAB" сегменты будут равны [2, 1] (2 плитки "A" и 1 плитка "B").
- Бэктрекинг — для каждого сегмента мы:
- пытаемся использовать плитку (уменьшаем количество плиток в этом сегменте);
Читать дальше →
ответить
Ссылка на задачу – 1718. Construct the Lexicographically Largest Valid Sequence.
📌 Условие задачи
Дано число n. Необходимо построить последовательность, удовлетворяющую следующим условиям:
- Число
1 встречается ровно один раз.
- Каждое число
i от 2 до n встречается ровно дважды.
- Для каждого числа
i > 1, два его вхождения в последовательность находятся на расстоянии ровно i.
- Среди всех возможных последовательностей требуется выбрать лексикографически наибольшую.
💡 Идея
Бэктрекинг — хороший способ решения данной задачи.
Чтобы получить лексикографически наибольшую последовательность, мы должны размещать сначала наибольшие числа.
🔄 Подробности метода
- Рекурсивно заполняем последовательность, начиная с первого свободного индекса.
- Используем массив
used, который отслеживает, какие числа уже размещены.
- Пропускаем занятые позиции.
- Проверяем возможность размещения числа заранее, прежде чем выполнять рекурсию.
Читать дальше →
ответить
Ссылка на задачу – 1352. Product of the Last K Numbers.
📌 Описание задачи
Необходимо создать структуру ProductOfNumbers, которая:
- Позволяет добавлять числа в поток (
add(num)).
- Вычисляет произведение последних k чисел (
get_product(k)).
Гарантируется, что ответы не приведут к переполнению 32-битного целого.
💡 Идея
Будем использовать префиксные произведения.
Это позволит получать результат за O(1), выполняя деление последних значений.
Но так как деление на 0 запрещено, придётся аккуратно отслеживать этот случай и сбрасывать произведения при появлении нуля.
⚙️ Подход
- Используем
Vec<i64> для хранения префиксных произведений.
- Добавление числа:
- Если
num == 0, очищаем хранилище, так как любое произведение после нуля будет равно нулю.
- Иначе умножаем предыдущее произведение на текущее число и сохраняем результат.
- Вычисление
get_product(k):
- Если
k больше количества сохранённых чисел, возвращаем 0.
- Иначе делим последнее префиксное произведение на значение
k шагов назад.
Читать дальше →
ответить
Ссылка на задачу – 3066. Minimum Operations to Exceed Threshold Value II.
📝 Описание задачи
Дан массив nums и число k. Мы можем выполнять следующую операцию, пока в массиве есть хотя бы два элемента:
- Взять два наименьших числа
x и y.
- Удалить их из массива.
- Добавить новое число
2·min(x,y) + max(x,y).
Необходимо найти количество операций, чтобы все числа в массиве стали ≥ k.
💡 Идея
Мы объединяем два наименьших числа, поэтому важно быстро находить и извлекать их.
Для этого можно использовать очередь с приоритетами (BinaryHeap), но в нашем случае можно действовать эффективнее.
🔹 Заведём две очереди (VecDeque):
orig_values — содержит исходные числа < k, отсортированные по возрастанию.new_values — хранит новые числа, появляющиеся в процессе операций, в гарантированно возрастающем порядке.
Благодаря двум упорядоченным очередям, минимальные элементы можно извлекать за O(1), а вся процедура будет работать эффективнее, чем с BinaryHeap.
Читать дальше →
ответить
Ссылка на задачу – 2342. Max Sum of a Pair With Equal Sum of Digits
📌 Условие задачи
Дан массив положительных чисел nums. Необходимо найти максимальную сумму двух различных элементов, у которых одинаковая сумма цифр. Если таких пар нет — вернуть -1.
💡 Идея решения
Вместо хранения всех чисел с одинаковой суммой цифр, достаточно хранить только максимальное из них.
Таким образом, при встрече нового числа с такой же суммой цифр можно сразу проверять, образует ли оно лучшую пару.
🔍 Подход к решению
- Используем массив
max_per_dsum, в котором храним наибольшее число для каждой суммы цифр.
- Максимальная сумма цифр для i32 — 82, но мы ограничиваем массив сотней для простоты.
- Обрабатываем
nums за один проход, применяя функциональный стиль с filter_map:
- вычисляем сумму цифр
d_sum для числа n;
- если уже есть число с таким
d_sum, определяем текущую сумму пары и сохраняем обновлённое максимальное число;
- если это первое число с данным
d_sum, просто сохраняем его в max_per_dsum;
filter_map отбрасывает неопределённые суммы пар (None), оставляя только валидные.
Читать дальше →
ответить
Ссылка на задачу – 1910. Remove All Occurrences of a Substring.
📌 Описание задачи
Даны две строки s и part. Нужно избавиться от всех вхождений part из s, выполняя следующую операцию:
- Найти самое левое вхождение
part в s и удалить его
- Повторять, пока
part больше не встречается в s.
🐢 Анализ наивного решения
Достаточно несложно быстро набросать следующее решение:
impl Solution {
pub fn remove_occurrences(mut s: String, part: String) -> String {
let P = part.len();
while let Some(idx) = s.find(&part) {
s.replace_range(idx..idx+P, "");
}
s
}
}
- Временная сложность такого решения в худшем случае достигает
O(N²/P)
Читать дальше →
1 ответ
Ссылка на задачу – 3160. Find the Number of Distinct Colors Among the Balls.
Описание задачи 😊
- Даны шарики с уникальными метками от
0 до limit (всего limit + 1 шариков)
- И список запросов, где каждый запрос имеет вид
[x, y]
- При каждом запросе шарик с меткой
x окрашивается в цвет y.
- После каждого запроса необходимо вернуть количество различных цветов, присутствующих среди раскрашенных шариков (неокрашенные не учитываются).
Идея 💡
Основная идея заключается в использовании двух хеш-таблиц:
ball_to_color – для хранения текущего цвета каждого шарика.color_counts – для подсчёта количества шариков каждого цвета.
Это позволяет за константное (в среднем) время обновлять информацию при каждом запросе и быстро определять число уникальных цветов.
Детали подхода 🔍
- Обновление цвета шарика:
- При выполнении запроса, если шарик уже был раскрашен, получаем его старый цвет и уменьшаем счётчик в
color_counts. Если счётчик для старого цвета становится равным нулю, уменьшаем количество уникальных цветов.
Читать дальше →
4 ответа
Ссылка на задачу – 3174. Clear Digits.
📌 Описание задачи
Дана строка s, содержащая буквы и цифры. Из неё возможно удалять цифры только путем выполнения следующей операции:
- Удалить первую найденную цифру и ближайший нецифровой символ слева.
Вернуть итоговую строку после итеративного выполнения указанной операции до исчезновения всех цифр.
💡 Идея
Достаточно легко придумать алгоритм, формирующий ответ справа-налево (просто запоминаем, сколько символов нужно скипнуть после встреченных цифр).
Мы же реализуем решение с прямым (слева-направо) обходом строки без необходимости переворачивания результата.
- Используем буфер (
buffer) для хранения промежуточного результата.
- Используем указатель
write_index, который отслеживает место для записи следующего символа.
- При встрече цифры уменьшаем
write_index (удаляем ближайший нецифровой символ).
⚙ Подробности подхода
- Инициализируем буфер размером
s.len() (заполняем заглушками '\0').
Читать дальше →
ответить
Ссылка на задачу – 2364. Count Number of Bad Pairs.
📌 Описание задачи
Дан массив nums, где пара индексов (i, j) называется плохой, если выполняется:
Требуется найти общее количество таких плохих пар.
💡 Идея
- Запишем условие хорошей пары:
j−i = nums[j]−nums[i]
- Переставляя слагаемые, получаем:
nums[j]−j = nums[i]−i
То есть если два индекса имеют одинаковое значение позиционной разности (nums[k] - k), – они образуют хорошую пару!
🛠️ Детали метода
- Создаём массив позиционных разностей:
pos_diff[i]=nums[i]−i
- Сортируем массив
pos_diff, группируя одинаковые значения.
- Используем метод
chunk_by для подсчёта частот одинаковых значений.
- Для каждой такой частоты
count, вычисляем количество хороших пар:
count×(count−1)/2
- Всего существует
n × (n - 1) / 2 пар, из них вычитаем хорошие пары и получаем ответ.
⏳ Асимптотика
- Время:
O(n·log n), так как сортировка доминирует над остальными операциями.
- Память:
O(n), так как храним pos_diff.
🔥 Хотя сортировка для подсчёта частот медленнее хеш-таблиц в асимптотике, на практике она быстрее из-за низкой константы!
📝 Исходный код
impl Solution {
pub fn count_bad_pairs(nums: Vec<i32>) -> i64 {
let n = nums.len() as i64;
// Compute adjusted values (nums[i] - i) and sort
let mut pos_diff: Vec<_> = nums.into_iter()
.enumerate()
.map(|(idx, num)| num - idx as i32)
.collect();
pos_diff.sort_unstable();
// Count good pairs using `chunk_by`
let good_pairs: i64 = pos_diff
.chunk_by(|a, b| a == b)
.map(|chunk| (chunk.len() as i64 * (chunk.len() as i64 - 1)) / 2)
.sum();
// Total pairs - good pairs = bad pairs
let total_pairs = n * (n - 1) / 2;
total_pairs - good_pairs
}
}
Tags: #rust #algorithms #math
ответить
Любимые факты об английском. Просто так, может, вы тоже порадуетесь. Ничего сверхъестественного, но удивляет, когда задумаешься.
"Ученик" ("школьник") по-английски "зрачок". То есть, "я весь внимание", буквально.
По-английски в радуге тоже семь цветов. Но это другие семь цветов. Синий и голубой ведь один и тот же цвет, а вот фиолетовые бывают разные.
"Государство" по-английски звучит примерно как "состояние дел". "Failed state" это не когда из крана перестает течь вода, а террористы мародерят в пригородах столицы, это просто констатация того, что некое "состояние дел" перестало самовоспроизводиться. "State", впрочем, даже в узком значении "состояние дел, связанное с управлением людьми на определенном куске земного шара" бывает не только таким, к которому мы привыкли (то, скорее, "nation state").
Слова "gore" в русском языке нет, хотя понятие, казалось бы, абсолютно базовое.
Слово "убийца" можно перевести на английский по меньшей мере 8 разными способами (slayer, killer, murderer, assassin, hitman, triggerman, manslayer, cutthroat). Наверное, есть больше. По-русски есть ещё душегуб, головорез (хотя он, скорее, thug, чем cutthroat) и позаимствованный "киллер". Вроде бы, всё?
Слова "зависть" и "ревность" почти взаимозаменяемы и носители языка считают нужным многословно пояснять разницу между ними, причем "зависть" (по крайней мере, в подобных заметках) считается более позитивным чувством. С другой стороны, "ревность" это вообще-то два разных слова, jealousy и insecurity, в зависимости от того, обладает ли испытывающий это чувство предметом вожделения в настоящий момент. "Insecurity", впрочем, это далеко не только "ревность". Сложна.
"Интеллигенция" по-английски "intelligentsia". В XXI веке употребляется далеко не только (и уже, по-моему, не столько) в значении "...в СССР", хотя раньше слово с таким значением почему-то никому не требовалось.
2 ответа
Ссылка на задачу – 1726. Tuple with Same Product.
📜 Описание задачи
Дан массив nums из различных положительных чисел. Нужно вернуть количество кортежей (a, b, c, d), таких что произведение a * b равно произведению c * d, при условии, что все элементы кортежа различны.
💡 Идея
- Для каждой уникальной пары элементов из массива nums вычисляем произведение и подсчитываем частоту его появления с помощью HashMap.
- Для каждого произведения, встречающегося больше одного раза необходимо учесть, что существует 8 уникальных вариантов составления кортежей:
a*b=c*d; a*b=d*c; b*a=c*d; b*a=d*c; c*d=a*b; c*d=b*a; d*c=a*b; d*c=b*a
- Соответственно, итоговый вклад, каждого произведения вычисляется как
4 * frequency * (frequency - 1)
🔍 Детали подхода
- Подсчет в HashMap:
- Используем два вложенных цикла для перебора всех уникальных пар
(i, j) с условием i < j и вычисляем их произведение.
- Результаты произведений сохраняем в
HashMap, где ключ — это само произведение, а значение — количество его вхождений.
- Расчет кортежей:
- Для каждого произведения с частотой больше
1, добавляем в итоговый результат значение
4 * frequency * (frequency - 1).
- Возврат результата:
Читать дальше →
1 ответ
Ссылка на задачу – 1790. Check if One String Swap Can Make Strings Equal.
Описание задачи 😊
Даны две строки s1 и s2 равной длины. Необходимо определить, можно ли сделать строки равными, совершив не более одного обмена символов в одной из строк.
Обмен — это операция, когда выбираются два индекса в строке и символы на этих позициях меняются местами.
Идея 😊
Основная идея заключается в поиске позиций, на которых символы в строках различаются.
- Если различий нет, строки уже равны.
- Если различия ровно в двух позициях, то проверяем, поможет ли один обмен исправить ситуацию.
- В остальных случаях (1 или более 2 отличий) сделать строки равными одним обменом невозможно.
Детали подхода 🚀
-
Сбор различающихся индексов:
- Пройдемся по всем индексам строк и соберем в вектор те индексы, на которых символы в s1 и s2 различаются.
При этом достаточно собрать максимум 3 индекса.
-
Проверка случаев:
- Нет различий: Если вектор пуст, строки равны.
Читать дальше →
ответить
Ссылка на задачу – 3105. Longest Strictly Increasing or Strictly Decreasing Subarray.
😎 Описание задачи
Дан массив целых чисел nums. Необходимо найти длину самой длинной последовательности, которая является либо строго возрастающей, либо строго убывающей.
🤔 Идея
Разбить массив на группы (чанки) по непрерывной монотонности (либо возрастающей, либо убывающей).
Для каждой группы вычислить её длину, а затем выбрать максимальное значение среди всех групп.
🚀 Детали подхода
- Разбиение на чанки:
Используем метод chunk_by для разбиения массива:
- Для строго возрастающей последовательности используем сравнение
a < b.
- Для строго убывающей последовательности используем сравнение
a > b.
- Вычисление максимальной длины:
- Для каждого набора чанков вычисляем длину каждой группы, выбираем максимальную длину для возрастающих и убывающих групп.
- Результат:
- Возвращаем максимум между максимальной длиной возрастающей и максимальной длиной убывающей последовательности.
⏱ Асимптотика
- Время:
O(n) — каждый элемент обрабатывается один раз при разбиении на чанки.
- Память:
O(1) — используется дополнительная память только для итераторов, не зависящая от размера входного массива.
📜 Исходный код
impl Solution {
pub fn longest_monotonic_subarray(nums: Vec<i32>) -> i32 {
// Group strictly increasing segments using chunk_by
let max_increasing_len = nums.chunk_by(|a, b| a < b)
.map(|c| c.len()).max().unwrap_or(0);
// Group strictly decreasing segments using chunk_by
let max_decreasing_len = nums.chunk_by(|a, b| a > b)
.map(|c| c.len()).max().unwrap_or(0);
max_increasing_len.max(max_decreasing_len) as i32
}
}
Tags: #rust #algorithms #iterators
1 ответ
Следуюшая задача для нашего обзора - 827. Making A Large Island.
Интересный способ для постобработки результатов стандартного поиска в графе.
📌 Описание Задачи
Дан n × n бинарный массив grid, где 1 — это суша, а 0 — вода.
Можно изменить ровно один 0 на 1, после чего необходимо найти размер самого большого острова.
Остров — это группа соседних единичек (соседи считаются по 4-м направлениям).
💡 Идея
1️⃣ Сначала находим и маркируем все острова, присваивая им уникальные ID.
2️⃣ Затем проверяем каждую клетку 0 и считаем, насколько большой станет остров, если заменить её на 1.
🛠️ Детали Подхода
- Маркируем острова с помощью
BFS
- Обход в ширину помечает все клетки острова уникальным
ID (начиная с 2).
- Запоминаем размер каждого острова.
Читать дальше →
ответить
Задача - 2493. Divide Nodes Into the Maximum Number of Groups.
📌 Постановка задачи
Дан неориентированный граф с n вершинами, возможно несвязный. Требуется разбить вершины на m групп, соблюдая условия:
✔ Каждая вершина принадлежит ровно одной группе.
✔ Если вершины соединены ребром [a, b], то они должны находиться в смежных группах (|group[a] - group[b]| = 1).
✔ Найти максимальное количество таких групп m.
✔ Вернуть -1, если разбиение невозможно.
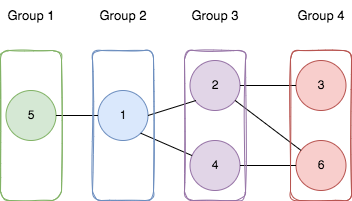
💡 Идея
- Граф можно корректно разбить на группы ↔ он двудольный.
- Максимальное количество групп связано с максимальной глубиной BFS в каждой компоненте.
- Мы проверяем BFS из каждой вершины, чтобы найти наилучший возможный корень для каждой компоненты.
🔍 Детали подхода
- Строим граф в виде списка смежности.
- Запускаем
BFS из каждой вершины (а не только из одной в компоненте) для:
- Проверки двудольности (по уровням
BFS).
- Поиска максимальной глубины
BFS (max_level).
- Определения уникального идентификатора компоненты (
min_index).
Читать дальше →
ответить
notq - коллективный блог. Я сделал его для людей, которые мне нравятся. Скорее всего, это и вы.
И лентой, и ранжированием комментариев управляют посетители с помощью голосования (примерно как на hackernews или на старом реддите). Пишите о чем угодно и как угодно. Вообще-то все свои, но некоторые иногда стесняются, поэтому можете писать анонимно.
Действует единственное правило: не пишите чего-нибудь такого, за что меня или вас посадят. Модерация есть, но предназначена только для решения этой задачи. Upd: правило отменено
notq - проект личный, некоммерческий, не связанный ни с какой компанией или организацией. Честно!
Баги и предложения о развитии можете кидать в комментарии.
Peace.
- Почему notq? В честь моей бывшей. В каком-то смысле. Потому что всего 4 буквы, не занято, вполне приличные ассоциации с нотами и заметками. Читается "нотка", а впрочем, читайте как хотите
- Что на логотипе? Глайдер из игры "Жизнь"
28 ответов
Следующая задача для разбора - 1462. Course Schedule IV
✨ Описание задачи
У нас есть numCourses курсов, пронумерованных от 0 до numCourses - 1.
Даны:
- Массив
prerequisites, где prerequisites[i] = [a, b] указывает, что курс a необходимо пройти перед курсом b.
- Массив запросов queries, где
queries[j] = [u, v] спрашивает: является ли курс u предшественником курса v.
Нужно вернуть массив булевых значений, где для каждого запроса ответ — true, если курс u является прямым или косвенным предшественником курса v; или false, если нет.
💡 Идея
Представим зависимости курсов в виде графа, где вершины — это курсы, а ребра указывают на зависимости между ними. Наша цель — определить, существует ли путь между двумя вершинами графа. Для этого можно использовать алгоритм Флойда-Уоршелла, чтобы вычислить транзитивное замыкание графа.
🛠️ Подробности подхода
- Инициализация матрицы зависимостей: Создаем булевую матрицу
n x n, где dep_matrix[i][j] обозначает, что курс i является предшественником курса j.
- Заполнение прямых зависимостей: На основе массива
prerequisites отмечаем прямые зависимости в матрице.
Читать дальше →
ответить
Задача, что мы рассмотрим сегодня - 2948. Make Lexicographically Smallest Array by Swapping Elements
📝 Описание задачи:
- Дан массив положительных чисел
nums и положительное число limit.
- Разрешено менять местами элементы массива
nums[i] и nums[j], если выполняется условие:
|nums[i] - nums[j]| <= limit.
- Необходимо получить лексикографически минимальный массив, выполняя такие операции любое количество раз.
Лексикографический порядок: Массив a меньше массива b, если на первой позиции i, где они различаются, a[i] < b[i].
💡 Идея:
Будем эксплуатировать следующие замечания:
- Элементы могут менять местами только внутри определённых групп, где (после её вырезания и сортировки) выполняется условие:
|nums[group[i+1]] - nums[group[i]]| <= limit.
- Индексная сортировка по значениям
nums поможет нас найти группы, внутри которых возможны перестановки.
- Сортировка каждой из этих групп может быть эффективно выполнена с помощью дополнительного индексного массива.
🔍 Детали подхода:
- Сортировка индексов: На первом шаге создаём массив
sorted_indices, заполняя его значениями [0, 1, ..., n-1]. Затем сортируем этот массив по значениям массива nums, чтобы определить относительный порядок элементов.
Читать дальше →
ответить
В очередной задаче для обзора - 802. Find Eventual Safe States нам предстоит найти вершины, не попадающие в циклы графа.
📋 Описание задачи
Нужно определить безопасные вершины в ориентированном графе.
- Безопасная вершина — это такая вершина, из которой невозможно попасть в цикл. Если из вершины можно попасть только в терминальные вершины или другие безопасные, она считается безопасной.
- Граф представлен в виде списка смежности, где
graph[i] содержит все вершины, в которые можно попасть из вершины i.
- Вернуть необходимо список всех безопасных вершин в возрастающем порядке.
- Граф из примера имеет безопасными вершины:
[4,5,6]
💡 Идея
Задача решается с помощью обхода графа в глубину (DFS) и вектора состояний.
Каждому узлу присваивается одно из трёх состояний:
Unseen (ещё не обработан);Processing (в процессе обработки; узлы, являющиеся частью цикла, остаются в этом состоянии и после обработки);Safe (безопасный).
🔍 Детальное описание подхода
Читать дальше →
ответить
В нашей новой задаче - 1765. Map of Highest Peak продолжим закреплять работу с семейством простых графовых алгоритмов.
📜 Описание задачи
Вам дана матрица isWater размером m×n, где:
isWater[i][j] == 1 указывает, что клетка — это вода.isWater[i][j] == 0 указывает, что клетка — это суша.
Требуется назначить высоты каждой клетке таким образом, чтобы:
- Высота каждой клетки была неотрицательной.
- Высота любой клетки с водой была равна 0.
- Абсолютная разница высот у соседних клеток не превышала 1.
- Максимальная высота в назначенной карте была как можно больше.
💡 Идея
Мы используем поиск в ширину с несколькими источниками (multi-source BFS), начиная с клеток воды (высота 0).
На каждом шаге ближайшие клетки суши получают высоту на 1 больше текущей.
Этот метод гарантирует, что все клетки суши получают наилучшую из возможных высот, что приводит к максимизации самой высокой высоты в матрице.
🛠 Подробности подхода
- Инициализация:
- Создаём очередь и добавляем в неё все клетки воды, помечая их высотой
0.
Читать дальше →
ответить
Сегодня в нашей задаче 2017. Grid Game требуется рассчитать оптимальную стратегию в игре с 2 участниками. И большая часть решения опять – "размышления на салфетке".
🖍️ Условие задачи
Дано: двумерный массив grid размером 2 x n, где grid[r][c] представляет количество очков в ячейке (r, c).
- Два робота начинают игру в ячейке
(0, 0) и должны достичь ячейки (1, n-1).
- Оба робота могут двигаться только вправо или вниз.
- Первый робот проходит от начальной точки до финиша, собирая все очки на своём пути.
- Затем второй робот выполняет аналогичный маршрут, при этом очки с пройденных первым роботом ячеек обнуляются.
Цель первого робота: минимизировать максимальное количество очков, которые сможет собрать второй робот.
💡 Идея
Легко увидеть, что только две стратегии второго робота могут оказаться оптимальными:
- Право → Вниз: Сначала пройти весь верхний ряд, а затем спуститься вниз на последней колонке.
- Вниз → Право: Спуститься вниз сразу, а затем двигаться вправо вдоль нижнего ряда.
Читать дальше →
ответить
В следующей задаче - 2661. First Completely Painted Row or Column можно не симулировать в лоб, и за счёт этого сэкономить память при решении (хоть и не получится асимптотически лучше).
📋 Описание задачи
- Нам дан массив
arr и матрица mat, содержащие числа от 1 до m * n.
- Массив
arr задаёт порядок закраски ячеек матрицы mat (закрашивается ячейка, содержащая указанное число).
- В следующем примере:
arr = [2,8,7,4,1,3,5,6,9], mat = [[3,2,5],[1,4,6],[8,7,9]]
Необходимо найти первый такой индекс i в массиве arr, при котором:
- Либо вся строка, либо весь столбец матрицы окажется закрашенным.
💡 Идея
Задачу можно переформулировать:
- Каждая строка и каждый столбец закрашиваются, если все элементы строки/столбца обработаны в порядке массива
arr.
- Получается, что для решения задачи нужно:
- Найти максимальный индекс появления значений из
arr для каждой строки/столбца.
Читать дальше →
ответить
Следующая задача 407. Trapping Rain Water II даёт возможность потренировать пространственное воображение (по крайней мере на этапе выбора адекватного для её решения алгоритма).
📋 Описание задачи
Дана 3D-сетка, представляющая высоты ячеек. Необходимо вычислить объем воды, который можно удержать после дождя. Вода может заполнять только области, окруженные ячейками с большей высотой.
💡 Идея
Мы рассматриваем каждую ячейку как часть сетки, где вода может стекать только в соседние ячейки с меньшей или равной высотой. Используя структуру данных непересекающихся множеств (Disjoint-Set или Union-Find), мы группируем соединённые ячейки и отслеживаем их связь с границами, чтобы определить, какие ячейки могут удерживать воду.
🛠️ Детали подхода
-
Представление и сортировка:
- Преобразуем все ячейки в список, где каждая ячейка представлена своей высотой и координатами.
- Сортируем ячейки по высоте в порядке возрастания.
-
Структура объединения множеств:
- Создаем дискретное множество для ячеек, добавляя виртуальный узел для границ сетки.
Читать дальше →
ответить
Страшилку "серой слизи" изобрел футуролог Эрик Дрекслер еще в прошлом веке. Суть идеи в том, что самовоспроизводящиеся наноботы, если упустить их из лаборатории, могут начать бесконечно копировать себя, и в результате Земля превратится в бесформенную "серую слизь", состоящую из гигантской массы нанороботов.
В 2024 году даже самые параноидальные исследователи экзистенциальных рисков относятся к "серой слизи" не слишком всерьёз. Мы не умеем делать самовоспроизводящихся наноботов и вряд ли научимся до того, как изобретём сильный искусственный интеллект который все равно нас уничтожит, с наноботами или без них.
Да?
Нет, первый реалистичный кандидат на роль "серой слизи" уже активно обсуждается, и именно в контексте "давайте сразу запретим, не дожидаясь, пока это начнут делать".
Чтобы понятно было, что это за зверь, почему его создание относительно реалистично, и чем всё это страшно, для начала напомню про понятие хиральности. Сложные органические молекулы могут быть несимметричными. В этом случае зеркальное отражение той же молекулы будет от неё отличаться. Например, для человека молекула "левой" хиральности может быть нормальным участником его метаболизма, а "правая" будет токсична.
Почему так происходит, ведь вроде бы законы химии инвариантны относительно зеркальной симметрии? Дело в том, в этом смысле почему-то несимметричны все живые существа. Аминокислоты, из которых состоят белки, в природе существуют почти исключительно в "левой" форме, а сахара, например, глюкоза, только в "правой". Хотя при замене хиральности у всех молекул, участвующих в реакции, ничего не поменялось бы, если заменить хиральность только у части из них, она может пойти совсем иначе, поэтому то, что жизнь несимметрична, важно.
Читать дальше →
3 ответа
Страница
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
