Задача - 2493. Divide Nodes Into the Maximum Number of Groups.
📌 Постановка задачи
Дан неориентированный граф с n вершинами, возможно несвязный. Требуется разбить вершины на m групп, соблюдая условия:
✔ Каждая вершина принадлежит ровно одной группе.
✔ Если вершины соединены ребром [a, b], то они должны находиться в смежных группах (|group[a] - group[b]| = 1).
✔ Найти максимальное количество таких групп m.
✔ Вернуть -1, если разбиение невозможно.
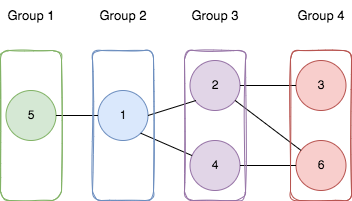
💡 Идея
- Граф можно корректно разбить на группы ↔ он двудольный.
- Максимальное количество групп связано с максимальной глубиной BFS в каждой компоненте.
- Мы проверяем BFS из каждой вершины, чтобы найти наилучший возможный корень для каждой компоненты.
🔍 Детали подхода
- Строим граф в виде списка смежности.
- Запускаем
BFS из каждой вершины (а не только из одной в компоненте) для:
- Проверки двудольности (по уровням
BFS).
- Поиска максимальной глубины
BFS (max_level).
- Определения уникального идентификатора компоненты (
min_index).
- Используем
HashMap для хранения максимальной высоты каждой компоненты.
- Если хотя бы одна компонента не двудольна, возвращаем
-1.
- Суммируем все найденные высоты и возвращаем результат.
⏳ Асимптотика
- Временная сложность:
O(N × E)
- Каждое ребро может быть обработано до
N раз, поскольку мы исследуем граф из каждой вершины.
- Пространственная сложность:
O(N + E)
O(N + E) для списка смежности.O(N) для BFS-структур (level, queue).O(N) для heights (HashMap, хранящий максимум одну запись на компоненту).
💻 Исходный код
use std::collections::{VecDeque, HashMap};
impl Solution {
pub fn magnificent_sets(n: i32, edges: Vec<Vec<i32>>) -> i32 {
let n = n as usize;
let mut graph = vec![vec![]; n];
// Build adjacency list representation of the graph
for edge in edges {
let (u, v) = ((edge[0] - 1) as usize, (edge[1] - 1) as usize);
graph[u].push(v);
graph[v].push(u);
}
let mut heights = HashMap::new(); // Store the maximum height for each component
// Iterate over all nodes, attempting to maximize height for each connected component
for start in 0..n {
if let Some((component_id, height)) = Self::bfs_check_and_find_height(start, &graph) {
heights.entry(component_id)
.and_modify(|h| *h = height.max(*h))
.or_insert(height);
} else {
return -1; // If any component is not bipartite, return -1
}
}
heights.values().sum()
}
// Performs BFS from `start` to determine if the graph is bipartite
// and find the maximum height in its connected component.
fn bfs_check_and_find_height(start: usize, graph: &[Vec<usize>]) -> Option<(usize, i32)> {
let mut level = vec![0 as i32; graph.len()]; // Track BFS levels
let mut queue = VecDeque::new();
queue.push_back(start);
level[start] = 1;
let mut max_level = 1; // Track the deepest BFS level reached
let mut min_index = start;
while let Some(v) = queue.pop_front() {
max_level = level[v]; // Update the deepest level reached
min_index = min_index.min(v);
// Traverse neighbors and check bipartiteness
for &u in &graph[v] {
if level[u] == 0 { // First visit to `u`
level[u] = level[v] + 1;
queue.push_back(u);
} else if level[u].abs_diff(level[v]) != 1 { // Bipartiteness check
return None // Graph is not bipartite
}
}
}
Some((min_index, max_level))
}
}
Tags: #rust #algorightms #graph #bfs