Ссылка на задачу — 2523. Closest Prime Numbers in Range.
📌 Описание задачи
Нам даны два целых числа left и right.
Нужно найти два ближайших простых числа num1 и num2 таких, что:
left ≤ num1 < num2 ≤ right- Оба числа простые
- Разница
num2 - num1 минимальна среди всех возможных пар
Если существует несколько пар с одинаковой разницей, выбрать пару с меньшим первым числом.
Если таких чисел нет, вернуть [-1, -1].
🧠 Идея
Будем просто итерироваться по парам соседних простых чисел в заданом диапазоне.
Но, так как простые близнецы (пары простых чисел, разница между которыми равна 2) встречаются довольно часто (их плотность примерно 1 / log²(n)) мы можем эффективно ввести условие раннего выхода, которое значительно улучшает среднюю производительность алгоритма.
🔍 Подход
- Обработка граничных случаев:
- Если
left ≤ 2 и right ≥ 3, сразу возвращаем [2, 3].
- Перебор чисел в диапазоне:
- Проверяем каждое число на простоту с помощью
is_prime(n), работающей за O(√n).
- С помощью
peekable() эффективно итерируемся по парам; обновляем лучшую пару, когда находим лучшую разницу.
- Ранний выход, если обнаружены простые близнецы (
diff == 2), так как они встречаются достаточно часто.
- Возвращаем лучшую найденную пару или
[-1, -1], если таких чисел нет.
⏱️ Анализ временной сложности
- Средний случай:
O(log²(left) ⋅ √right)
- Из-за плотности простых близнецов
(1 / log²(n)) мы ожидаем найти такую пару после проверки O(log²(left)) чисел.
- Каждая проверка на простоту работает за
O(√n).
- Худший случай:
O((right - left) ⋅ √right).
🗂️ Анализ пространственной сложности
O(1): Используются только несколько целочисленных переменных, без дополнительных массивов или структур данных.
📝 Исходный код
impl Solution {
pub fn closest_primes(left: i32, right: i32) -> Vec<i32> {
if left <= 2 && right >= 3 {
return vec![2, 3]; // Handle the smallest prime pair case early
}
let mut min_diff = i32::MAX;
let mut best_pair = vec![-1, -1];
// Iterate over primes using a peekable iterator
let mut primes = (left..=right).filter(|&n| Self::is_prime(n)).peekable();
while let (Some(left_prime), Some(&right_prime)) = (primes.next(), primes.peek()) {
let diff = right_prime - left_prime;
if diff < min_diff {
min_diff = diff;
best_pair = vec![left_prime, right_prime];
if diff == 2 { // Early exit for twin primes
break;
}
}
}
best_pair
}
// is_prime checks whether a given number n is prime.
fn is_prime(n: i32) -> bool {
let mut p = 2;
while p * p <= n {
if n % p == 0 {
return false;
}
p += 1 + p % 2; // Increment by 1 if p=2, otherwise skip even numbers
}
true
}
}
⚡ Оптимизация времени выполнения:
- В Rust мы можем предварительно вычислить весь битсет
IS_PRIME на этапе компиляции.
- Это позволяет проверять простоту чисел за
O(1), а среднее время выполнения алгоритма сокращается до O(log²(left)).
- Благодаря этому наша реализация становится ультра-быстрой! 🚀
// is_prime checks whether a given number n is prime.
// Uses compile-time Eratosthenes Sieve for fast lookup.
#[allow(long_running_const_eval)]
fn is_prime(n: i32) -> bool {
const MAX_PRIME: usize = 1_000_000;
const INT_SIZE: usize = 128; // Store 128 numbers per element
const IS_PRIME: [u128; MAX_PRIME / INT_SIZE + 1] = {
let mut is_prime = [u128::MAX; MAX_PRIME / INT_SIZE + 1];
is_prime[0] &= !3; // Mark 0 and 1 as non-prime
let mut p = 2;
while p <= MAX_PRIME {
if (is_prime[p / INT_SIZE] & (1 << (p % INT_SIZE))) != 0 {
let mut d = 2 * p;
while d <= MAX_PRIME {
is_prime[d / INT_SIZE] &= !(1 << (d % INT_SIZE));
d += p;
}
}
p += 1 + p % 2;
}
is_prime
};
let n = n as usize;
(IS_PRIME[n / INT_SIZE] & (1 << (n % INT_SIZE))) != 0
}
Теоретико-числовое замечание
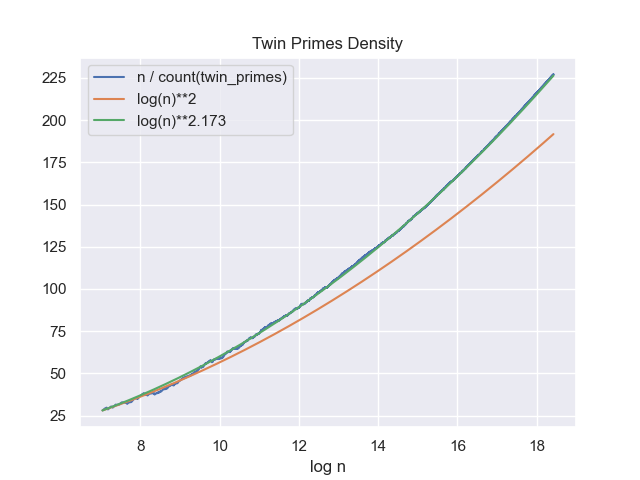
На самом деле плотность простых близнецов - открытый вопрос (как и то конечно ли их количество).
Однако численный эксперимент показывает, что на обозримом горизонте (до 1 миллиарда) вероятность встретить пару простых близнецов близка к O(1/log²·¹⁷³n).
Именно эту оценку в разборе я для простоты упростил до квадратичной зависимости от логарифма.
Tags: #rust #algorithms #math #optimization