Ответ спасен из Яндекс.Кью
Часто на Кью люди сначала растекаются мыслью по древу, а потом отвечают на вопрос (или не отвечают). Попробую быть хорошим мальчиком и сделать наоборот. Это, конечно, не так.
В целом не верю в деление людей на гуманитариев и технарей, да и любые подобные ярлыки. Они позволяют сохранять энергию, если у вас класс в 35 человек и по 8-10 уроков в день. Тогда, наверное, да, удобно налепить на часть ярлык «гуманитарий» и давать им некоторый минимум. Но это же нечеловеческие какие-то условия, нельзя людей в них загонять, ни учеников, ни учителей.
Мозги у людей устроены очень по-разному. Кстати, на моей статистике - безо всякой связи с делением на гуманитариев и негуманитариев. Стереотипы про системное мышление точно не работают - знаю массу историков с потрясающе выстроенными логическими связями и привычкой идеально систематизировать знания, и знаю массу математиков и физиков, которые мыслят очень воздушно.
Я был бы готов эту концепцию обсуждать с позиций нейрофизиологии - но вот беда, насколько я знаю, с качественными исследованиями на эту тему небогато. How comes.
Ну а теперь можно и по древу. Я человек, проконтактировавший с отечественной системой образования с 90-х и до этого времени в полную силу. Все, что может случится в школе плохого или хорошего - я об этом знаю на личном опыте. Давайте я совсем ужасы рассказывать здесь не буду, это тема для отдельного разговора. В частности, гуманитарные познания у меня, как и у большинства моих сверстников, крайне низки.
Мое гуманитарное образование представляет из себя следующий коктейль.
-
Курс истории. Лучшая его часть была мировой историей в седьмом классе, которую читала мне учительница литературы. Затем началось бесконечное повторение отечественной истории и истории Татарстана (я вообще из Казани). Повторение - потому что суммарно я раза 4 прошёл историю России с Рюрика до где-то Брежнева обрывками (никакого после), раза 3 - историю Татарстана примерно от именьковской культуры до Булгар. Ещё раз - мировая история у меня была только в 7 классе.
-
Курс обществознания. Совсем обрывками.
-
Литература. Тут бывал по-разному, но в среднем тоже не могу похвастаться. А, ну и татарская литература, о которой я, наверное, знаю чуть больше, чем средний россиянин.
И это примерно все. Подозреваю, что я не уникален - по ощущениям, это похоже на среднюю картину для моего сверстника. И если по математике или физике полученный объём знаний в целом неплохо (но и не лучше всех, конечно) смотрится на мировом уровне, то в гуманитарных науках все не очень здорово. Конечно, все перечисленное я дополнял как мог сам. Но в целом сейчас я ощущаю то место, где во мне должны быть гуманитарные знания, как огромную зияющую дыру. Причём даже не с позиций фактических знаний, их-то можно подучить, а с позиций методологии. Что и как мы делаем.
Читать дальше →
ответить
Статья спасена из Яндекс.Кью
Давайте начнём сегодня с того, что просто посмотрим на фото:

Ну и что, это же туманность Sh2-279, мы её сразу узнали издалека - скажете Вы.
Красивая? Конечно, это ж астрономия, здесь все красивое. Посмотрите внимательно на звезды. Они же как будто сказочные, вовсе не огромные газовые шары, а фото, вообще-то сделано профессиональным телескопом. Отсюда вопрос - почему звезды на фото остроконечные? И, кстати, ведь Вы когда смотрите на небо, тоже видите их не округлой формы? Сначала Вам может показаться, что звезду Вы видите точкой, но если Вы внимательно всмотритесь в небо, Вы увидите её именно остроконечной. В чем же дело?
Все дело в дифракции света. Вспомним это простейшее явление. Свет — это волна. Когда свет от удалённого источника проходит сквозь щель или вокруг какого то предмета, световые волны искажаются таким образом что на луче остаётся отпечаток щели или предмета. Например, так будет выглядеть дифракция света, прошедшего через прямую щель:

А теперь найдите источник света - светильник, лампочка - все что угодно. И прищурьтесь. Давайте угадаю, что Вы видите? Что-то такое:

Вот. В этом случае щель у нас горизонтальная, поэтому дифракция вытягивает свет в перпендикулярную пунктирную линию.
А теперь представьте, что отверстие в виде +. Что мы увидим? Сложите первые две картинки:

А если отверстие в форме круга:

Все, что мы видим выше - результат прохождения луча света сквозь какое-то отверстие или вокруг какого то предмета.
Так почему же мы видим звезды такими, как будто у нас на глазах какие-то щели или предметы? А потому что в человеческом глазе есть маленькие, так сказать, несовершенства на хрусталиках - «линии шва» на местах, где сходятся ткани, из которых состоит хрусталик. Они и оставляют свой узор на проходящем свете. Так как у каждого глаза свои индивидуальные линии шва, в виде всяких пересекающихся различным образом маленьких линий, каждый глаз, даже левый и правый одного человека, будет видеть звезды своей уникальной формы, в зависимости от хрусталика и его линий шва. Так что каждый Ваш глаз будет видеть звезды только одной формы.
А в начале, кажется, я говорила про фото с телескопа. Почему же телескоп тоже видит звёзды остроконечными? У него-то нет хрусталиков! Посмотрите например на снимок Хаббла - Туманность Киля:
Читать дальше →
3 ответа
Ответ спасен из Яндекс.Кью
Есть такие ресурсы. Разумеется, секретные они только для «широкой публики», поскольку совсем уж секретной информации, прямо вот для всех-всех-всех, – не бывает вовсе. При этом вопрос я буду понимать буквально, считая, что он задан не для «бла-бла “за жизнь“», а вполне серьёзно — для решения проблемы. Слово «выгодные» из вашего вопроса требует объяснения. Выгода прямая – купить подешевле? Или непрямая – купить с меньшими затратами времени, сил и нервов? Замечу, что в процессе жизни непрямая часто превращается в прямую. Я буду писать про то и другое. И оговорка: пишу про Петербург: региональных/местных условий и особенностей ещё никто не отменял.
Начну с мифологии. С тех «секретных ресурсов», которых нет. Бывают «агенты», прости господи, которые потенциальным клиентам говорят, что у их агентств есть какие-то секретные базы квартир. Если речь идёт не о квартирах за… за миллионов хотя бы… 100 (не могу определиться, подробней напишу ниже), то таких баз/ресурсов – нет. А «агент» – «гражданин соврамши» и во все секреты его посвящает кукла Полишинель. На всякий случай, для справки: баз покупателей таких объектов тоже нет. На рынке, где купить легче, чем продать, их и быть не может.
А какие же «секретные ресурсы» есть на вторичке? Собственники пентхаузов с видом на Стрелку Васильевского острова или вилл ценой в «ярд» чаще всего не горят желанием увидеть объявление о продаже их объекта на, прости господи, «Авито». «Деньги любят тишину», так зачем же всем подряд, в том числе возможным мошенникам и ворам, знать, что кто-то продаёт очень дорогое жильё – это же не «светская хроника» для саморекламы. Сарафанное радио? Ну… Бывает, наверное. В узком кругу Сарафанное радио между «коллегами» по толщине кошелька»? Ну… Можно, наверное. В узком кругу. Иногда очень узком (тот ещё «ресурс»). И поэтому сотню-другую «лимонов» можно «нечаянно» и упустить.
Есть агентства, которые работают по таким объектам. Вот они-то, скооперировавшись, и организуют для общения между собой такие «секретные ресурсы», куда «Посторонним вход воспрещён». Покупатель переплатит на комиссионных? Да, но если не эти комиссионные, то вы подходящего объекта (выгодного!) можете и вовсе не найти.
«Секретные ресурсы», причём отнюдь не элитной (или «элитной» в понимании массового первичного рынка). Начну с неосновного: это сайты, специализирующиеся на продаже так называемых подрядных квартир.
Не все покупатели понимают, но на самом деле слово «застройщик», особенно если речь идёт о крупных, обозначает не собственно строительную компанию, а девелопера – организатора строительства. Название крупного застройщика – это часто, и даже скорее, бренд, «торговая марка»а конкретный жилищный комплекс строит его «дочерняя компания», которая, в свою очередь, для разных конкретных работ часто нанимает специализированную компанию – то есть подрядчика.
Читать дальше →
ответить
Статья спасена из Яндекс.Кью
Один из основателей и третий президент США, соавтор декларации независимости, Томас Джефферсон был деистом (то есть верил в Бога-создателя, никак не вмешивающегося в свое создание), но находил в жизнеописании Христа много интересного и верил в него как в историческую личность. Поэтому он написал собственную версию Евангелия, и даже не одну, а несколько, последнюю в 1820 году в возрасте 77 лет.

С 1904 года и вплоть до 1950-х годов решением Сената каждый вновь избранный американский сенатор получал копию этой книжки.
1 ответ
Ответ спасен из Яндекс.Кью
Программирование — очень широкая область. Поэтому сначала определитесь с направлением. Подумайте, какая сфера в программировании интересна именно вам. Чем бы вы хотели заниматься: создавать сайты, делать игры или мобильные приложения? Чтобы в этом разобраться, попробуйте каждую из сфер на практике. Например, пройдите несколько коротких онлайн-курсов.
Дальше рассмотрим несколько сфер и языков программирования в них. Это далеко не все сферы и, тем более, не все языки. Но этот список даст начальное представление о логике выбора сферы и языка в ней.
Создание фронтенда сайтов
Коротко: начните с HTML, CSS и JavaScript, а там видно будет.
Фронтенд — это та часть сайта, которую видит пользователь. Например, прямо сейчас вы читаете ответ на вопрос на сайте Яндекс.Кью. Всё, что вы видите в браузере — это фронтенд, сделанный фронтенд-разработчиком.
Во фронтенде выбор языков для старта невелик. Начать в любом случае придётся с HTML, CSS и JavaScript. После их изучения вам, вероятно, станет ясно, куда идти дальше. Обычно это изучение одного или нескольких фреймворков из списка: React, Vue или Angular.
Создание бэкенда веб-сервисов
Коротко: начните с Python, с него проще всего начать.
Вернёмся к примеру с фронтендом сайта Яндекс.Кью. Вопросы и ответы пользователей хранятся не в вашем браузере, а на удалённом компьютере — сервере. Чтобы сервер сохранял вопросы и ответы и отправлял их в браузер, нужно сделать бэкенд. Над бэкендом трудится бэкенд-разработчик.
В отличие от фронтенда здесь очень широкий выбор языков. Бэкенд можно делать практически на чём угодно. Самые популярные языки сегодня: Python, Java, C, C++, Ruby и JavaScript. Если у вас нет опыта программирования, я бы советовал начать с Python. А позже всегда можно переключиться на что-то другое.
Создание мобильных приложений
Коротко: начните со Swift для iOS и c Kotlin или Java для Android.
Мобильными разработчиками сделаны все приложения в вашем телефоне.
В мобильной разработке есть два больших направления: iOS и Android (есть ещё Windows Phone и другие, но я бы не советовал с них начинать, так как их рынок гораздо меньше). От выбора направления зависит выбор языка программирования. В iOS популярны языки Swift и Objective-C. В Android — Kotlin и Java. Также есть языки и технологии, которые позволяют делать приложения сразу под обе платформы. Это, например, JavaScript в связке с React Native или Dart в связке c Flutter. Они подойдут, если вы переходите из веб-разработки в мобильную, но начинать с них я бы не советовал — для новичков это сложно.
Создание игр
Коротко: для браузерных игр — HTML, CSS и JavaScript. Для мобильных — перечитайте блок про создание мобильных приложений. Для компьютерных игр придётся выбрать из C++, C# или Java.
Читать дальше →
ответить
Статья спасена из Яндекс.Кью
Пейтингерова скрижаль (названа так по имени владельца — коллекционера Конрада Пейтингера) была создана в XIII веке эльзасским монахом. Эта карта — копия римской карты III-V веков. Вообще, это не совсем карта, это схема всех дорог Римской империи (их примерная общая длина около 200 тыс. км.). На схему нанесены 555 городов, ~3500 достопримечательностей, места, где можно отдохнуть и сменить лошадей, отмечены горы, леса и водоёмы.
Скрижаль состоит из 11 пергаментных листов, на которых изображен мир от Британии до Индии и Китая. Размер самой карты 6,75 м на 0,34 м!
По сути своей, Пейтингерова скрижаль — это такой древний прообраз Яндекс/Гугл карт, позволяющий примерно проложить путь от одного пункта до другого.
Хранится Пейтингерова скрижаль в Вене в Австрийской национальной библиотеке.
Скрижаль в огромном разрешении можно посмотреть здесь (15+ Мб):
https://upload.wikimedia.org/wikipedia/commons/5/50/TabulaPeutingeriana.jpg?fbclid=IwAR3V5kDDyZ5y4WA3Qjqy-nG809k9CFaDNQeBgppFPdtKmC8riGu8nbPdsHw

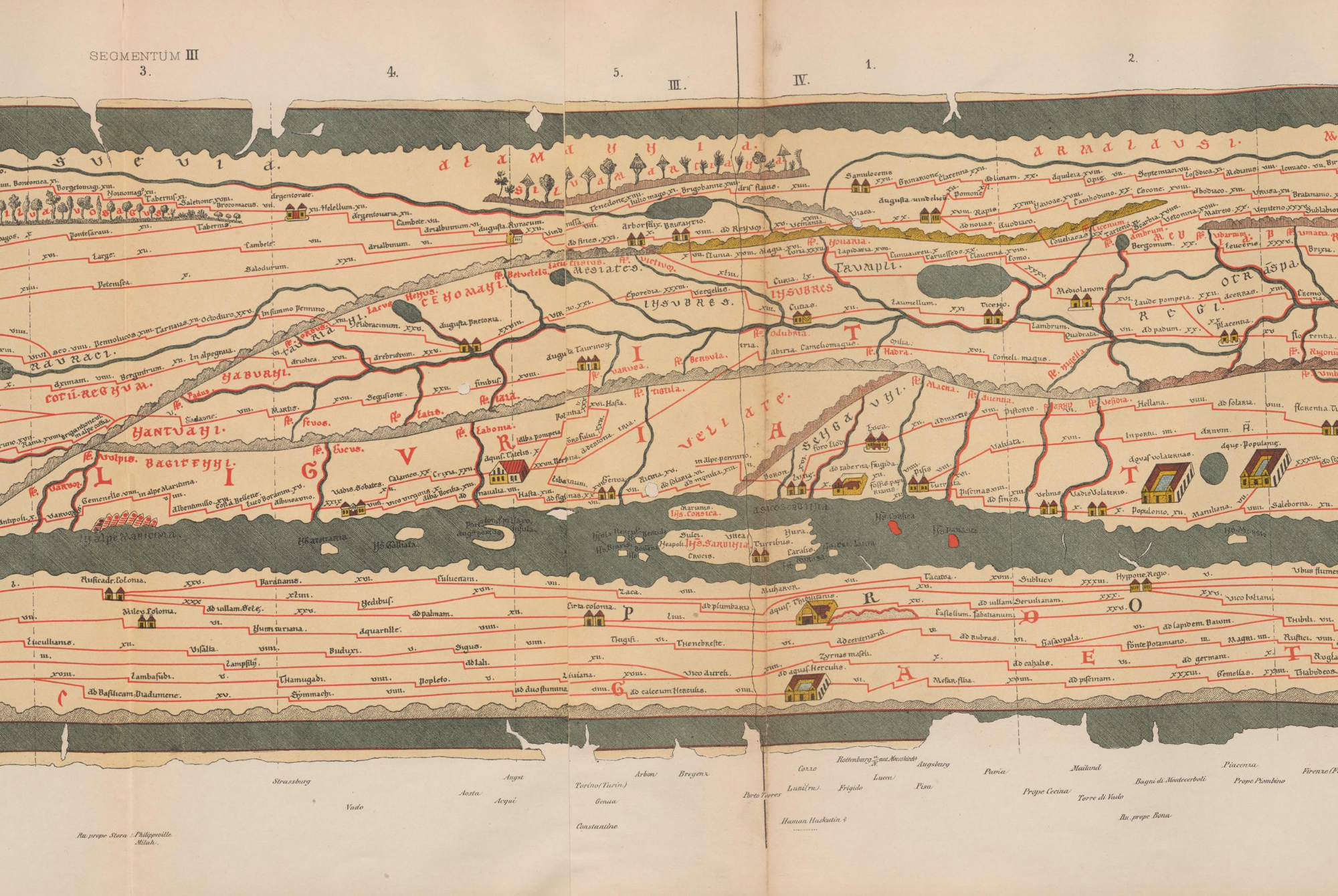
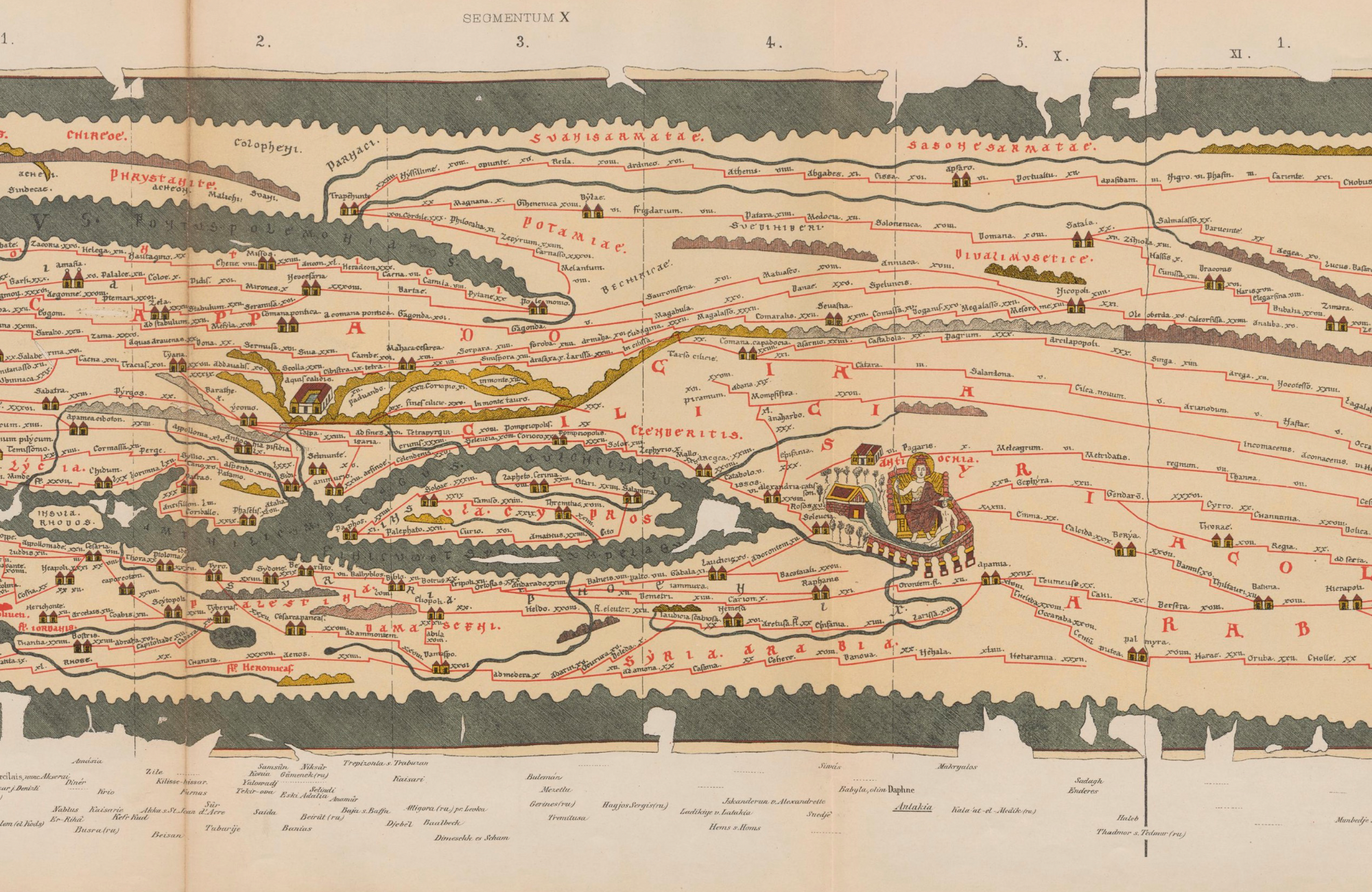
PS
Оказывается, есть классный планировщик маршрутов, составленный на основе этой скрижали:
https://omnesviae.org/
ответить
Ответ спасен из Яндекс.Кью
Настоящая математика слишком сложна для детектива и слишком абстрактна, чтобы помогать раскрывать реальные преступления. Тем не менее, кое-какие идеи, в разной степени притянутые за уши, в голову приходят!
- Про тонкости определения понятия "вероятности". Знаменитая история с мошенниками, которые рассылали по почте случайные биржевые советы и прекращали рассылать их тем адресатам, кому прислали неверный. С точки зрения оставшегося в итоге одного из 1024 адресатов они десять раз подряд оказались правы. Сверхъестественная точность! Вероятность того, что таинственный отправитель случайно угадал движение акций 10 раз подряд, меньше одной тысячной!! Конечно же, получив одиннадцатый совет -- вложить крупные деньги в компанию этих самых мошенников -- бедняга последовал ему с воодушевлением.
- Можно подумать над каким-то применением "принципа Дирихле". Сам принцип выглядит просто, почти тривиально: если N+1 кроликов посадить в N клеток, то в какой-то клетке окажется больше одного кролика. Но в детективе, думаю, вполне можно замаскировать его так, что соответствующее открытие будет неожиданным; например, количество кроликов и количество клеток раскрыть в разных частях повествования. Допустим, семья олигарха собралась на его даче в составе 13 человек за одним столом и в какой-то момент пила чай из одинаковых чашек; но разве бывают сервизы на 13 персон, спросит себя детектив в решающий момент? Или, например, девять главарей мафии якобы уехали куда-то на двух майбахах; в общем, понятно
- Есть по крайней мере две криптографические идеи, эпизоды на основе которых можно представить себе в современном детективе. Во-первых, "наивный" подстановочный шифр элементарно расшифровывается и несложно описать, как именно, без всяких теоретических тонкостей. Именно его обычно и придумывают люди, не знакомые с криптографией, ну а с чего бы книжным террористам или бандитам быть математически грамотными? Правда, Артур Конан Дойль уже написал рассказ "Пляшущие человечки" как раз в точности об этом, но в другом антураже и с какими-то изменениями идея может и сыграть.
- Во-вторых, существуют способы, общаясь у всех на виду, обменяться информацией так, что никто, кроме двух участников разговора, не сможет узнать, какой именно. Собственно, ваш браузер и большинство сайтов в интернете (особенно те, на которых вы вводите платежные данные) общаются друг с другом именно так. Конкретный математический способ сложноват для широкой публики, но можно представить себе и описать его физический аналог. Допустим, Ваня и Маша могут обмениваться посылками, в том числе, например, ключами или шкатулками, закрытыми на замок. Любой ключ, который они так посылают, недоброжелатель может перехватить и скопировать, а любую шкатулку, закрытую на замок, открыть, если скопировал ключ от этого замка (но не может украсть или взломать -- не знаю, как уж это объяснить в тексте детектива, но условия математической задачи такие). Могут ли Ваня и Маша как-то обмениваться посылками так, чтобы содержимое хотя бы некоторых шкатулок осталось секретом от этого недоброжелателя, если изначально общих ключей у них нет? Ответ - да!
Читать дальше →
ответить
Статья спасена из Яндекс.Кью
Две статьи одного и того же автора, способные дать пищу для мозга на недели (это не преувеличение).
- What's Wrong with Social Science and How to Fix It: Reflections After Reading 2578 Papers.
- How I Made $10k Predicting Which Studies Will Replicate
На перечисление всего, что из них можно узнать, даже в виде "тизеров" меня, боюсь, не хватит, но я все равно начну.
I. DARPA поддерживает многомиллионную программу DARPA SCORE, в рамках которой, в частности, работает сайт replicationmarkets.com (вот их самоописание). Чтобы было понятней, насколько это безумие, попробуем перевести на русский:
- исследовательское подразделение Министерства Обороны решает побороться с кризисом воспроизводимости (!) в социальных науках (!!)
- для этого спонсирует воспроизведение сотен (!!!) научных работ и конкурс, в рамках которого анонимные нерды через интернет участвуют в симуляции фондовой биржи, "товарами" на которой являются предсказания того факта, будет ли воспроизведен такой-то результат (всё, у меня закончились восклицательные знаки)
Это настолько странное, "ботанское" и "целящееся в Луну" использование денег военных, что даже непонятно, с чем сравнить. ИПМ им. Келдыша до такого ещё очень далеко.
II. В этом конкурсе люди вроде автора статей выше не просто участвуют, а вкладывают совершенно фантастическое количество усилий за негарантированные деньги порядка месячной зарплаты программиста в тех краях.
III. В процессе чтения первой статьи можно получить интуитивное, висцеральное понимание того, насколько общественные науки в их текущем состоянии сломаны. Словами самой же статьи:
Приятно критиковать плохую науку с вершины абстрактной горы. Вы слышите о результатах, которые не воспроизводятся, о методологиях, которые кажутся немного глупыми. "Им стоит улучшить используемые ими методы", "p-хакерство - это плохо", "нужно изменить систему стимулирования", - заявляете вы, как Зевс, со своего трона в облаках, а затем переходите к чему-то другому.
Но настоящее погружение в социальные науки, это море мусора, дает вам более осязаемую перспективу, более интуитивное отвращение и, возможно, даже чувство лавкрафтовского благоговения перед самим масштабом всего этого
IV. В процессе чтения второй статьи можно оценить (с высоты очень птичьего полёта, конечно), как выглядит инструментарий трейдера даже в такой игрушечно-модельной области, и заодно попробовать понять, почему постановка prediction markets именно такая, а не более простая: не просто "получает приз тот, кто угадывает итог лучше всех", а именно с симуляцией торговли "ценными бумагами" в процессе.
На этом пока всё, если хотите о чем-то подробнее, го в комментарии
ответить
Ответ спасен из Яндекс.Кью
Совсем напрямую нельзя, потому что в байтах измеряют память компьютеров, а она устроена не так, как человеческая (подробней об этом ниже).
Но можно попытаться ответить на два похожих вопроса:
1) если бы мы попытались использовать человеческий мозг как устройство хранения информации для , на какой объем мы могли бы рассчитывать?
2) каким должен быть объем памяти у компьютера, способного мыслить, как человек?
Сначала о том, в каком именно смысле компьютерная память устроена иначе, чем человеческая, и почему это важно для ответа на наш вопрос. Попробуйте запомнить два числа: 5555555555 и 5714204664. Хотя они и одного порядка и требуют для своей записи одного количества цифр, но человеку, конечно же, проще запомнить первое. А вот компьютеру совершенно всё равно.
Человеческая память неотделима от поиска закономерностей и ассоциаций. Человеку проще запоминать что-то логичное, рифмующееся, закономерное, обращающееся к предыдущему опыту, достраивать уже имеющуюся картину мира. Компьютерной памяти важен только объём информации, который в байтах и выражается, а вот для человеческой байт байту рознь, и это мягко говоря.
Перейдем теперь к вопросам, на которые ответить можно!
1. Если бы мы попытались использовать человеческий мозг как устройство хранения информации для , на какой объем мы могли бы рассчитывать?
Человеческая память неточна. Вы же помните, как выглядят лошади? Конечно, помните! Даже если нет, найдите в интернете фото лошади и посмотрите на него. Попробуйте теперь эту лошадь воспроизвести по памяти, хотя бы с искажениями. Не очень получается, правда? А ведь это всего-то одна фотография, у вас даже на телефоне их сотни, небось.
Мировой рекорд запоминания числовой последовательности -- примерно 80000 знаков числа пи. Человек, который это сумел, уникум, это чудовищно, невероятно много: просто прочитать эти цифры вслух займёт целый день. И в то же время это совсем мало, меньше ста килобайт. Можно смело сказать, что 100 килобайт это верхний предел ответа на наш первый вопрос. У вашего компьютера оперативная память в десятки тысяч раз больше.
В общем, использовать человеческую память как устройство хранения информации, аналогичное компьютерной памяти, это очень плохая идея.
2. Каким должен быть объем памяти у компьютера, способного мыслить, как человек?
Буквально совсем недавно, в 2019-2020 годах, в искусственном интеллекте появилась очень интересная тенденция: выглядит так, что нейронные сети определенной разновидности (так называемые трансформерные языковые модели) оказываются тем умнее, чем больше они в байтах. GPT-2, которая "весит" единицы гигабайт, умнее, чем модели, "весившие" сотни мегабайт, и уже способна порождать вполне связные тексты на человеческом языке. А GPT-3, сеть, которая "весит" примерно терабайт, местами "рассуждает" пугающе по-человечески.
Читать дальше →
ответить
Статья спасена из Яндекс.Кью
Сегодня я прочитал описание джан (состояний в буддийской медитации) и с удивлением обнаружил, что с детства умею достичь первой джаны, только не знал, что это так называется.
Мой способ не тот, которому обычно учат и, возможно, он неправильный. Например, даже ко второй джане я не умею перейти, а их, на минуточку, обещают восемь. Зато моим способом сделать это очень просто, мне хватает нескольких минут, и это интересный опыт, позволяющий на собственной шкуре понять, что всё это не булшит, в этом определенно что-то есть. Хотя в интернетах пишут, что "даже достижение первой дхьяны — это выдающееся достижение", вот это как раз полный булшит, по-моему.
Чтобы достичь первой джаны, нужно лечь в тихом месте на удобную горизонтальную поверхность и закрыть глаза. Дальше нужно избавиться от беспокоящих мыслей. Конечно, невозможно "не думать о белой обезьяне", но мне лично для этого достаточно сказать самому себе "об этом я подумаю чуть позже", не гнать, но и не раскручивать никакую мысль, пусть себе приходят и уходят.
Затем нужно расслабить все мышцы по очереди. Прямо мысленно обратить внимание на каждую область тела, начиная, например, с кончиков пальцев ног, и далее двигаясь выше. Порядок не очень важен и анатомическая тщательность тоже, у человека мышц очень много, наверняка вы пропустите что-нибудь, но это неважно. Через несколько минут вы начнете чувствовать себя подвешенным в какой-то полуневесомости. Сосредоточьтесь на этом ощущении, и скоро оно разрастётся и превратится в приятное, сильное и странное, ни на что не похожее чувство освобождения и перехода в другую реальность.
Это может звучать как шутка -- эзотерическое описание обычного процесса засыпания -- но я пишу всерьёз, джана это не сон, а собственное состояние, совсем на него не похожее, отличающееся и от сна, и от бодрствования и относительно них находящееся в каком-то третьем перпендикулярном направлении. Я не мистик и уверен, что нейрофизиологически всё это вполне объяснимо, что-нибудь там про альфа-ритмы и прочие резонансы нейронов.
В таком состоянии я оставался обычно не больше пары минут, потому что по какой-то причине становилось страшновато. Выйти из первой джаны просто, нужно лишь этого захотеть -- пошевелить руками-ногами, например.
Интересно, у вас получится?
3 ответа
Ответ спасен из Яндекс.Кью
Очень многое зависит и от самого человека, и от ВУЗа:
-
вполне можно успешно работать программистом, обучившись этому с нуля
-
успешных программистов с высшим образованием гораздо больше, чем без него. Но вовсе не факт, что именно благодаря обучению. Скорее, взаимосвязь косвенная: умному человеку и поступить куда-нибудь проще, и учиться, и программирование осваивать.
-
есть некоторые разделы программирования, которым очень сложно обучиться самостоятельно, не отучившись хотя бы пару курсов в техническом ВУЗе: машинное обучение и data science, теория формальных языков и компиляторов, теория оптимизации
-
мест в индустрии, где эти разделы программисту по-настоящему пригодятся, не так много, но они одни из самых престижных и высокооплачиваемых
-
практические навыки программирования гораздо быстрее нарабатываются в реальной работе, чем при любом обучении
-
но при этом в некоторых ВУЗах создается и поддерживается среда, в которой самые талантливые студенты много программируют, соревнуются друг с другом, друг у друга учатся, проходят стажировки в ведущих компаниях и к четвертому-пятому курсу уже могут горы сворачивать. Такие "звёзды" в индустрии очень ценятся. При этом тот же ВУЗ вполне могут успешно заканчивать и люди, ни строчки кода за годы обучения не написавшие, так что корочки сами по себе ни о чем не говорят
ответить
Статья спасена из Яндекс.Кью
Очень часть на Q задают вопросы вроде "может ли любитель придумать что-то новое в математике" — в самых разных вариациях. Я, если честно, не уверен что этот пост кого-то в чём-то сможет убедить, но решил позволить себе немного порассуждать на тему.
С одной стороны, конечно, многие великие математики нового времени были любителями (непрофессиональными математиками). Например Пьер Ферма был по основной профессии юристом, его блистательный корреспондент Марен Мерсенн — монахом, Христиан Гольдбах — скорее чиновником и так далее. При этом их заслуги в математике (ну и вообще в естествознании) — неоспоримы.
Строго говоря, феномен успешного любителя — встречается и сейчас. Например пару лет назад обсуждали одного профессионального биолога, который сумел придумать хитрый контр-пример к одной задаче из комбинаторной теории групп. Или вот, как утверждает хабр в одной старой задаче Лебега удалось продвинуться любителю Филиппу Гиббсу (мне, если честно, не удалось убедиться в том, что Гиббс действительно любитель, но можно и на слово поверить). Задача состояла в том, чтобы отыскать фигуру наименьшей площади, которая может накрыть собой любую плоскую фигуру диаметра 1. Саму работу можно посмотреть здесь.
В тоже самое время есть и всякие наблюдения, которые не требуют вообще никаких предварительных знаний. К примеру скатерть Улама, которую обнаружили от скуки.

Всего-то, выписав числа как на картинке, Улам отметил простые числа. И заметил, что оказывается они очень чётко группируются. Это позволило скажем анализировать простые числа "генерируемые" многочленами ax^2+bx+c.
Так что даже и в современной математике частенько рассматривают вопросы с достаточно низким порогом вхождения. Я бы вообще отметил комбинаторную геометрию и выпуклую геометрию, как примеры таких разделов математики. Есть, правда, и теория чисел, в которой формулировки задач очевидны даже школьнику, но вот современные методы работы — неочевидны зачастую и профессиональному математику. Скажем доказательство великой теоремы Ферма — считается одним из самых сложных результатов 20-го века.
Так что же, любой сообразительный человек может пойти и решить что-нибудь эдакое, обессмертив своё имя как блистательного математика и утереть нос всяким зазнайкам?
Нет.
Primum. Математика в 21 веке — не та что была в 19-м. Дело не только в революции, которую в математике совершил Гильберт сотоварищи на рубеже 19-20 веков, поставив математику на аксиоматические рельсы, но и в том, что над известными простыми вопросами люди думают как раз с 19-го века. Так что простые решения по большей части уже нашли. Что более важно, разработано огромное количество общих результатов, которые хорошо описывают стандартные закономерности привычных объектов: свойства дзета-функции помогают разбираться с простыми числами, оптимальное управление — с минимаксными задачами и т.д.. Таким образом, для решения большинства "простых вопросов" нужно на самом деле искать ответы на куда более сложные. Хороший пример — та же теорема Ферма. По сути, Уайлс получил куда более общий результат (см. тут и замечательную книгу Сингха) — известный как проблема Таниямы-Шимуры.
Читать дальше →
ответить
Ответ спасен из Яндекс.Кью
Эрроу пытался придумать способ справедливо обобщать индивидуальные предпочтения (то есть создать справедливую избирательную систему). Но у него не получилось; причем дело не в том, что он плохо старался, а в том, что это невозможно в сделанных предположениях. Эрроу математически строго сформулировал теорему о том, что именно невозможно. По традиции эта теорема называется теоремой о невозможности демократии, а иногда парадоксом Эрроу.
В рамках теоремы рассматриваются N (больше двух) индивидуумов; скажем, граждане одной страны, жители одного многоквартирного дома или компания друзей. У них есть несколько альтернатив; скажем, кандидаты в президенты, варианты ремонта в доме, или способы провести выходной день вместе. Важно, что осуществиться может только одна альтернатива, ее нужно выбрать вместе.
По условию теоремы считается, что каждый индивидуум может упорядочить эти альтернативы по предпочтительности. Допустим, мы собрали списки предпочтения у всех индивидуумов (провели голосование) и хотим по этим спискам построить общий список предпочтений. Иными словами, на основе индивидуальных предпочтений выработать коллективное. Вот Эрроу и попытался это сделать математически строго. Он еще потребовал выполнения некоторых условий, которые представляются вполне разумными.
-
Универсальность: каждый избиратель предоставляет один и только один список своих предпочтений, и при этом волен упорядочить альтернативы как ему угодно.
-
Отсутствие диктатора: общий список предпочтений не должен определяться только одним индивидуумом без учета предпочтений всех остальных.
-
Независимость от посторонних альтернатив. Это свойство можно по-разному формулировать, например так: если в общем списке предпочтений кандидат А стоит выше кандидата В, а потом в число кандидатов вошел еще Х (или наоборот, кого-то вычеркнули), то А все равно останется выше В.
-
Единогласие: если все избиратели ставят А выше В, то и в общем списке предпочтений А должен стоять выше В.
Далее Эрроу математически доказал, что не существует избирательной системы, которая удовлетворяла бы всем этим требованиям.
Смысл теоремы Эрроу не в том, что это приговор демократии, а в том, что она дала стимул дальнейшим исследованиям. К "Очевидно разумным" предположениям стоит присмотреться внимательнее.
Мы теперь знаем, что не вполне рационально действуем, когда делаем выбор. Мы иногда не можем определиться, какой вариант предпочтительнее, не можем сравнить альтернативы. Бывает, что предпочтения есть, но они нетранзитивны: например, я предпочитаю мороженое каше, кашу котлете и котлету мороженому; такие предпочтения нельзя упорядочить. Предпочтения могут быстро меняться. На сытый желудок у меня одни предпочтения, а на голодный другие.
Читать дальше →
5 ответов
Статья спасена из Яндекс.Кью
Здесь было все: непопулярный монарх, делавший все, чтобы настроить против себя всю страну, вмешательство извне, миф о почти полной бескровности переворота, споры между победителями и кардинальные изменения после революции. Все это - революция 1688 года в Англии, она же "Славная революция" она же - "Первая современная революция" (по словам Стивена Пинкуса).

Король Яков II, вступивший на английский престол после смерти брата - Карла II - в 1685 году, сразу же начал с крайне непопулярных шагов. Оправдывал он их тем, что с самого начала столкнулся с двумя восстаниями, во главе одного из которых стоял его незаконнорожденный племянник - Джеймс Скотт герцог Монмут. В ответ на это он начал создавать регулярную армию, подчиняющуюся лично ему, состоящую во многом из католиков из Ирландии и Шотландии. Началось тотальное вытеснение англикан с руководящих постов и замена их католиками (причем на всех уровнях власти). Аналогичные шаги предпринимались и в отношении судебного корпуса. Кроме того, король лично составлял списки кандидатов в парламент, а затем используя "административный ресурс" старался добиться их избрания. Наконец, он стремился более жестко контролировать англиканскую церковь, тогда как в отношении католической наоборот, всячески поддерживал ее. В целом политику Якова II можно назвать "католической модернизацией", целью которой было превращение его в абсолютного монарха, по образцу Людовика XIV (с которым он, кстати, вступил в союз, носящий антинидерландскую направленность). В 1687 году он также выпустил два акта о веротерпимости, разрешив свободное исповедание как католикам, так и радикальным протестантам, против которых были гонения еще со стороны англикан. Но поддержки со стороны этих радикалов король так и не получил. В итоге, к 1688 году против Якова II было настроено подавляющее большинство населения Англии, но по разным причинам: простых людей больше раздражала прокатолическая политика короля, тогда как высшие слои были больше обеспокоены перспективами получить абсолютную монархию и лишиться права влиять на политику. Однако потенциальному выступлению против короля не хватало лидера...

И тут надо перенестись на континент, где жил штатгальтер Нидерландов, а по совместительству племянник и зять Якова II Вильгельм Оранский. И его очень сильно беспокоил союз Англии и Франции, направленный против Нидерландов. Вполне резонно опасаясь, что в случае совместных действий этих двух держав, шансов на победу у него не будет, он был настроен на поиск любых шагов, могущих ослабить противников. Взгляд его упал на Англию, где недовольство против короля Якова II становилось все более заметным. Еще больше оно усилилось после того, как у него родился сын, который отодвинул в очереди престолонаследия супругу Вильгельма Марию. Это означало, что никаких изменений в политике Англии в ближайшее время не будет, а значит она по-прежнему будет угрозой для Нидерландов. И тогда Вильгельм начал действовать. Как пишет Саймон Дженкинс
Читать дальше →
ответить
Ответ спасен из Яндекс.Кью
Всего при археологических раскопках в Месопотамии было найдено более 500 тыс. глиняных табличек. Из них математических - около 400. Это были преимущественно школьные математические задания и решения задач.
Сколько относится к шумерскому периоду я не нашел данных. В основном это были тексты Вавилонского периода и позже, т.е. позже 1800 г до н.э.
Точно ш шумерам (до их семитизации) относят появление 60-дестиричной системы. Причём интересно, что шумеры первыми придумали позиционную запись чисел. От 1 до 60 они использовали обычную 10-ричную систему, а вот после 60 - уже привычную нам запись - позиционную. Т.е. место в числе определяло степень, в которую надо было возвести 60. У них не было 0 , поэтому были трудности в расшифровке записи. Позднее, уже вавилонянами придумали знак нечто в виде "пустоты". Были и другие проблемы записи и чтения, но они решались анализом контекста записи.
Для облегчения расчётов имелись справочные таблицы по умножению, обратным числам (шумеры не делили, а находили обратное число, которое умножалось на первый сомножитель), квадратам. Эти таблицы помогали чисто механически производить расчёты очень быстро.
А считали они много. Это было нужно и в торговле, и при сборе налогов, и в строительстве, и для предсказания смены сезонов, особенно для разлива.
И, что очень важно было для шумеров - это разметка полей, т.е. геометрия. Посл паводка все межевые знаки смывались и надо было размечать поля заново. Что способствовало развитию геометрии.
Однако, если судить по текстам табличек, все геометрические расчёты шумеры предпочитали делать в алгебраической форме. Поэтому нередко они могли запросто, условно говоря, к грушам прибавлять яблоки.
Много внимания уделялось единицам счисления. Поскольку в каждом городе-государстве были свои единицы, которые не совпадали между собой.
Что касается теоремы Пифагора, то время её открытия установить нельзя, но уже в старовавилонский период (1900-1600 гг до н.э.) она была хорошо известна и использовалась для землемерных работ. Сведения из стереометрии применялись для решения задач с сыпучими материалами и жидкостями (определения объёмов).
В целом про шумерский период известно очень мало и фрагментарно. Все сведения по истории математики относятся уже к более поздним историческим эпохам.
ответить
Статья спасена из Яндекс.Кью
И всё.
https://sandiegozoowildlifealliance.org/species/platypus
Представляете, несмотря на всю глобализацию, осталось на Земле что-то интересное, что не поместили в контейнеры Maersk и не развезли по всему миру
ответить
Ответ спасен из Яндекс.Кью
В том виде, в котором вы подаете этот вопрос - конечно же нет. В сражениях Древности (будем говорить об Античности) индивидуальные качества бойцов значили весьма немного: исход боя решала коллективная подготовка, умение действовать всем строем сообща, сплоченность и - самое главное - дисциплина. По крайней мере, в идеале и у греков с римлянами.
Неправильно здесь применять сам термин "свалка". Если один из противников дошел до состояния свалки, то он уже проиграл. Потому что россыпь индивидуальных бойцов - пусть они хоть МСМК по всему на свете - не сделает ничего против сплоченного строя даже посредственных воинов. Беспорядочная свалка возможна только в том случае, если одна из сторон уже одержала победу и, например, преследует противника.
Таким образом, бой идет не столько между конкретными бойцами по обе стороны, сколько строй против строя. По опыту своих тренировок с реконструкторами римской армии, ты не всегда даже видишь того, кто стоит против тебя. Ты делаешь то, чему тебя учили, стараешься соблюдать порядок и равнение, наносишь удары тоже, как тебя учили и надеешься, что ваш строй окажется крепче.
Безусловно, у любых воинов в любую эпоху были свои писанные и не очень нормы поведения, этика и этос. Но следование им не ставит перед воинами проблему победы или поражения. Как правило, они касаются отношения к уже побежденным, к мирным людям и так далее. То есть, вне боя, хотя есть и те, что предписывают определенную модель поведения и в сражении.
Кстати, замечательный ответ на Ваш вопрос может дать сама античная традиция. Ознакомьтесь с легендой о братьях Горациях. По легенде, три брата-римлянина сражались с тремя братьями Куриациями из города Альба-Лонга. Когда двое из троих Горациев были убиты, все трое противников намеревались сразить и последнего. Но последний из Горациев стал убегать от них и, пользуясь ранами своих противников, стал побеждать одного врага за другим, поскольку те гнались за ним с разной скоростью. Даже если учесть легендарный характер этого сюжета, в нем все равно очень хорошо прослеживаются нормы поведения. Если этот сюжет пересказывали и он пользовался популярностью, значит это одобряли.
ответить
Статья спасена из Яндекс.Кью
Интересное обсуждение на реддите. Краткий пересказ: для червя-нематоды c.elegans известна его полная "коннектома", т.е. описаны все 302 нейрона (червь не очень умный) и все связи между ними. В течение 10 лет команда энтузиастов пытается сделать компьютерную модель червя, которая реагировала бы на стимулы так же, как сам этот червь. Если бы нейронная сеть червя была устроена так же, как искусственные нейронные сети, т.е. каждый нейрон имел бы взвешенные входы и функцию активации, это было бы довольно просто.
Утверждается, что на самом деле каждый биологический нейрон вычисляет довольно хитрую функцию, на языке DL более-менее точно описываемую только целой сеткой с 5-8 слоями и 1000 "нейронами". Прямое моделирование радикально осложняется тем фактом, что "веса на входах" нейрона могут меняться, это пока что невозможно наблюдать на живой особи, и даже теоретически неизвестно, как понять, что в этих изменениях будет соответствовать "стадии обучения", а что "стадии применения".
В комментах есть даже супер-пессимистичное мнение, что один нейрон устроен сложнее любой нашей искусственной нейросетки (честно говоря, оно кажется мне диким и очевидно неверным, но удивительный факт состоит в том, что существует специалист в предметной области, который его придерживается).
ответить
Ответ спасен из Яндекс.Кью
Искусствоведы не ищут смыслы. Искусствоведы удостоверяют авторство, датировки, подлинность работ, происхождение материалов, технику, источники аллюзий, положение того или иного предмета в общем поле.
На искусствоведа учатся пять лет, плюс два года аспирантуры, плюс большинство знакомых искусствоведов защищали потом диссертацию. Искусствоведов подвергают такой же выучке, как историков, археологов, переводчиков с латыни или учёных социальных наук — плюс, это в какой-то степени всегда немного междисциплинарная область, то есть для искусствоведа нормально на досуге почитывать финансовую историю, геологию, эволюционную науку, мало ли что.
К счастью, чтобы понимать картины, искусствоведом быть не обязательно. Смыслы большинства предметов искусства искать просто не нужно, потому что они или лежат на поверхности, или легко находятся в общей литературе, если конечно человек её хотя бы по диагонали читал.
Общее правило — всегда, в ста процентах случаев — в том, что предмет должен рассматриваться в контексте истории. Нормальной истории. Не популярной истории, не националистического бреда, не теледокументалок. Общее знание истории позволяет делать неплохие догадки даже по периодам, которые человек плохо знает (ключевое слово — догадки).
Иными словами, всё это упирается в базовый культурный фундамент и навык работы с источниками, который по идее должен быть у каждого человека, закончившего вышку. Почему он на практике настолько плохо распространён — не знаю.
ответить
Статья спасена из Яндекс.Кью
Жил-был Ули Прагер, сын отельера. Ули родился в 1916 году, а в 1948 году в достаточно, но не очень голодной послевоенной не воевавшей Швейцарии Ули шёл по мосту и увидел, как чайка вырывает хлеб из рук человека. По немецки чайка - Möven, а удар - pick.
Ули открыл отель с дурацким (как считала его Мама) названием Mövenpick. А потом ещё и мороженое такое сделал.
Сейчас я живу в гостинице Mövenpick в Москве. Тут классно. Мама Ули Прагера, похоже, ошиблась. Ули умер в 2011 году, отель Mövenpick открылся в Москве в 2020. У чувака все получилось.
ответить
Ответ спасен из Яндекс.Кью
Правильнее сказать не "зачем нужна", а что она возникает всякий раз, как возникает точка отсчета и ориентиры.
Всякий раз как вы спрашиваете прохожего, например: "А где здесь почта?" - он скажет, - "пройдите туда столько-то, потом поверните за угол, там пройдите еще столько-то и найдете почту".
Всё у вас уже возникла система координат. Нулевая точка то, где вы находитесь, а туда куда вы направляетесь - это точка с известными координатами.
Разумеется, если вы начинаете сообщать свои координаты другим - вам тоже нужны какие-то ориентиры. Например, я стою у входа в метро на станции такой-то. Всё вы задали точку отсчета и обозначили место. Пока не числами, но вы подразумеваете, что собеседник знает как ему в своей системе отсчета добраться к ориентиру.
Или, например, билеты в театре продаются по местам - вам же надо как-то обозначить какой ряд, какое место вам дали. Всё - система координат.
Ладно, прекрасно. А теперь представьте, что вы в путешестии - либо на корабле, либо где-нибудь в бескрайней пустыне. И у вас нет никаких ориентиров где вы сейчас конкретно - кроме солнца и звезд. Вот примерно для таких случаев люди придумали разметить весь наш земной шар на меридианы и парраллели и взять некоторые более-менее естественные точки отсчета. Поскольку их можно было вычислить в любом месте мира, достаточно было имет хороший доступ к обозрению неба - это оказалось хорошей практикой.
А паралельно с этим развивался математический аппарат всего этого, чтобы было удобно и хорошо ориентироваться не только на глобусе, но и на плоской карте.
Ну а после всего этого Рене Декарт придумал, что геометрические задачи через координатный метод решать гораздо проще, чем через классические древнегречиские методы.
ответить
Статья спасена из Яндекс.Кью
У Монголии нет выхода к морю и официально нет военно-морского флота, но так было не всегда.
Когда-то монгольский флот был одним из крупнейших в мире. Потом большая часть флота затонула во время монгольского вторжения в Японию. Во время советской власти, в 1930-х годах, флот был создан вновь. К 1990 году монгольский военно-морской флот состоял из одного судна, расположенного на крупнейшем озере страны, состоял из 7 человек и был самым маленьким флотом в мире. А в 1997 году он был приватизирован и для покрытия расходов возил экскурсии по озеру.
ответить
Ответ спасен из Яндекс.Кью
Число Грэма это не самое большое число в мире, это "самое большое натуральное число, когда-либо использовавшееся в серьезном математическом доказательстве". Грэм это фамилия, кстати, а не сокращение, писать его БОЛЬШИМИ БУКВАМИ не имеет смысла.
Как уже написали в другом ответе, изобрести число больше тривиально, например, прибавить к числу Грэма любое другое натуральное число, или умножить его на что-нибудь, или в квадрат возвести, да мало ли операций над натуральными числами.
Однако же существует интересная конструкция, позволяющая определить натуральные числа намного больше не только числа Грэма, но и вообще любого числа, которому можно дать определение в формате "произведите такие-то операции и получите результат".
Эта конструкция называется Busy Beaver, и строится она так:
Возьмем какой-нибудь язык программирования. Возьмём все возможные программы на этом языке длины не более N байт. Их конечное число: в самом деле, их точно не более 256^N. Большая часть из них вообще не запустится, часть запустится и ничего не выдаст, или выдаст какой-то бред, или ошибку, часть зациклится, а какие-то программы выдадут в итоге некое число. Поскольку программ всего конечное количество, будет конечным и множество всех чисел, которые мы можем так получить. Максимальное из этих чисел назовём BusyBeaver(N).
(я здесь упрощаю, язык программирования в исходном определении не любой, а вполне конкретный, машины Тьюринга, и "символов" у них нет, но всё это не принципиально)
Последовательность BusyBeaver с ростом N растёт катастрофически быстро. Даже просто оценить, насколько быстро она растёт, буквально невозможно. В самом деле, допустим, мы нашли формулу, ограничивающую её рост. Ну, например, BusyBeaver(N) < 256^N^N^N^N. Запишем эту формулу в виде программы. Пусть эта программа займет M символов. Выберем N такое, что N > M+lg(N) (чтобы запись числа N тоже уместилась в ту же программу) и посчитаем с помощью неё оценку BusyBeaver(N). Ого, мы пришли к противоречию: программа длины M+lg(N) выдала число больше, чем BusyBeaver(N)!
То есть какое бы мы ни придумали определение "последовательности Очень Больших чисел", которое можно записать в виде вычислимой процедуры, BusyBeaver всё равно растёт быстрее.
Небольшое отступление. Так, стоп, что-то здесь не то, почему это не противоречие? Вот возьмем и определим SmizzyBeaver(N) = BusyBeaver(N)+1, она ещё быстрее будет расти.
Это не противоречие, потому что последовательность BusyBeaver невычислима. Буквально не существует процедуры, позволяющей взять N и вычислить BusyBeaver(N) (поэтому эти числа известны только для очень маленьких N).
Ну вот, после того, как всё сказано: ответ на исходный вопрос простой, запишите вычисление числа Грэма в виде программки и возьмите BusyBeaver(длины этой программки), это число будет больше не только числа Грэма, но и любых чисел, которые можно вычислить программой той же сложности. BusyBeaver(не очень-то большого числа, соответствующего пределу рабочей памяти человека) представить себе буквально невозможно.
ответить
Статья спасена из Яндекс.Кью
Сегодня человечество отправило в космос одно из лучших своих изобретений -- 6.5-метровый инфракрасный телескоп Джеймса Уэбба (планета подешевела на 10 млрд $).

Что значит инфракрасный, почему это важно и чем отличается от привычного оптического телескопа? Человек видит глазом в достаточно узком (оптическом) диапазоне длин волн электромагнитного спектра (почему так -- об этом я писал здесь) от 400 до 700 нм. Допустим, мы хотим увидеть самые ранние галактики. Но они очень далеко от нас, и фотонов от них приходит не так много -- нужно большое зеркало, чтобы сфокусировать как можно больше фотонов (у телескопа Уэбба зеркало ~6.5 м). Как известно -- чем дальше галактика, тем её спектр дальше смещён в красную часть диапазона электромагнитных длин волн, а значит -- инфракрасный диапазон представляет особый интерес.
Но! Чем дальше от нас объект исследований -- тем больше препятствий у света по пути от него. Межгалактическая среда, галактики, облака газа и т.д. -- всё это находится на луче зрения. Окей, пучок фотонов достиг нашей Галактики, но и наша межзвёздная среда тоже состоит из газа и в зависимости от траектории -- свет испытывает различное взаимодействие с веществом.

Хорошо наблюдать внегалактические объекты перпендикулярные плоскости нашей Галактики. Иначе -- поток от объекта поглощается достаточно сильно. А сквозь ядро Галактики в оптике мы от далёкого объекта вообще ничего не разглядим. Наблюдать в плоскости Млечного Пути необходимо в инфракрасных лучах (они поглощаются гораздо слабее). Но тому препятствует земная атмосфера, в ней содержится водяной пар H₂O. Вода -- источник жизни! И поглощения в ИК-области. Более того, в ИК-диапазоне светятся здания, сооружения, астрономы. Да и сам телескоп и инструменты. А это шум, который не помогает в исследованиях. То есть, даже сами приборы необходимо охлаждать целиком! При этом, инфракрасное стекло не должно треснуть. Стоимость таких сложных приборов – не трудно догадаться – очень высока. А раз атмосфера срезает нам ИК-лучи, то инфракрасному телескопу прямая дорога только в космос! Звучит недёшево.
БЕЗ ПРАВА НА ОШИБКУ.
Телескоп отправляется куда дальше своего младшего брата – телескопа им. Хаббла (высота ~600 км) – в точку Лагранжа на расстоянии ~1.5 млн км от Земли. А значит -- к нему не отправить экипаж астронавтов на случай поломок или модернизации. С другой стороны, будет хорошая радиосвязь, а телескоп можно будет наблюдать в полночь. За месяц ожидается разворачивание солнцезащитного козырька (размером с теннисный корт), чтобы избежать нагрева телескопа и инструментов (температура которых снижена до –223°), дабы избежать собственного ИК-излучения. Чтобы выиграть как можно больше света -- зеркало покрыто слоем золота с высоким коэффициентом отражения. Ещё одно принципиальное отличие от оптических инструментов касается детекторов излучения. Привычные кремниевые детекторы излучения уже не годятся -- их чувствительность падает в области микрона (10000 Å). Уэбб чувствует от 0.6 мкм до 28 мкм.
Читать дальше →
ответить
Ответ спасен из Яндекс.Кью
Ну, как слышали — плохо, учитывая не только подшлемник, но и вообще уровень шума вокруг. Посему приказы подавались не только и не столько голосом, а при помощи духовых инструментов и барабанов. Плюс очень большую роль играли знамёна как визуальный сигнал. А вообще — на эту тему есть очаровательная история.
Дело было во время Восьмой Итальянской войны: битва при Ранти 13 августа 1554 года.
Ведя в атаку кавалерию, герцог де Гиз заметил, что один из его офицеров (служил в чине лейтенанта) нарушил строй, вырвавшись вперёд. По всей видимости, докричаться до него в грохоте атаки было невозможно, поэтому герцог ударил подчинённого мечом по шлему.
После боя герцогу донесли: лейтенант сильно оскорблён таким поступком командира. Дело пахнет дуэлью, ведь оба они люди благородные. Ситуация не из приятных.
Но герцог де Гиз поступил мудро. Он вызвал к себе лейтенанта, причём говорить решил не с глазу на глаз, а при всём высшем командовании, включая короля Франции. И заявил: дескать, я нанёс вам удар, но вы не должны считать это оскорблением, поскольку моей целью являлось заставить вас не скакать в атаку слишком быстро. Вот если бы наоборот, я вас принуждал не трусить таким образом — это было бы оскорблением. А так мои действия лишь подчёркивают вашу великую отвагу!
Присутствовавшие согласились, что лейтенанту и правда не на что обижаться, раз он оказался слишком храбр, а не наоборот. Инцидент был исчерпан, дуэль не состоялась.
ответить
Страница
1
2
3
4
5
6
7
8
