Ссылка на задачу — 3108. Minimum Cost Walk in Weighted Graph.
📌 Описание задачи
- Дан неориентированный взвешенный граф с
n вершинами и m рёбрами.
- Каждое ребро представлено тройкой
[u, v, w], означающей, что существует ребро между u и v с весом w.
- Определим стоимость пути между двумя вершинами как битовое
AND всех рёбер, пройденных на пути (вершинам в таком пути разрешено повторяться).
- Для каждого запроса
[s, t] требуется найти минимальную AND-стоимость пути между s и t.
- Если пути не существует, ответ
-1.
Пример
- Входные данные:
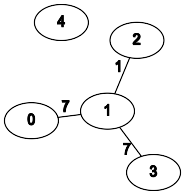
n = 5; edges = [[0,1,7],[1,3,7],[1,2,1]]; query = [[0,3],[3,4]]
- Результаты:
[1, -1]
- Объяснение:
- Наилучший путь от
0 до 3: 0 → 1 → 2 → 1 → 3.
- Путей из
3 в 4 не существует.
- Графическая интерпретация:
💡 Идея
- Так как каждое новое ребро пути его стоимость не увеличивает, то внутри каждой компоненты связности стоимость минимального пути будет одинаковой (достаточно определить путь, проходящий через все рёбра компоненты связности).
Читать дальше →
1 ответ
Задача - 2493. Divide Nodes Into the Maximum Number of Groups.
📌 Постановка задачи
Дан неориентированный граф с n вершинами, возможно несвязный. Требуется разбить вершины на m групп, соблюдая условия:
✔ Каждая вершина принадлежит ровно одной группе.
✔ Если вершины соединены ребром [a, b], то они должны находиться в смежных группах (|group[a] - group[b]| = 1).
✔ Найти максимальное количество таких групп m.
✔ Вернуть -1, если разбиение невозможно.
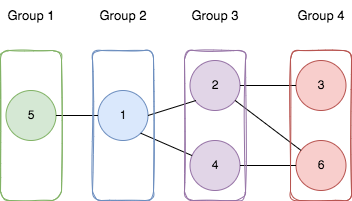
💡 Идея
- Граф можно корректно разбить на группы ↔ он двудольный.
- Максимальное количество групп связано с максимальной глубиной BFS в каждой компоненте.
- Мы проверяем BFS из каждой вершины, чтобы найти наилучший возможный корень для каждой компоненты.
🔍 Детали подхода
- Строим граф в виде списка смежности.
- Запускаем
BFS из каждой вершины (а не только из одной в компоненте) для:
- Проверки двудольности (по уровням
BFS).
- Поиска максимальной глубины
BFS (max_level).
- Определения уникального идентификатора компоненты (
min_index).
Читать дальше →
ответить
Сегодня мы решаем задачу 3243. Shortest Distance After Road Addition Queries I
Постановка
В задаче требуется вычислить кратчайший путь от города 0 до города n-1 после каждой из последовательных добавлений новых дорог в граф. Изначально города соединены цепочкой дорог, и после каждой операции добавляется новая односторонняя дорога между двумя городами. Необходимо после каждой операции находить кратчайшее расстояние от города 0 до города n-1.
🔍 Идея
Данное решение использует оптимизированный подход с поочередным обновлением расстояний с помощью BFS и ранним выходом при нахождении цели (города n-1). Мы обновляем граф и расстояния только при необходимости, что позволяет сократить количество ненужных вычислений и повысить производительность.
📚 Обзор решения
-
Инициализация графа и расстояний:
- Сначала создаем список смежности
succ, который представляет дороги между городами, инициализируем его так, чтобы города были соединены цепочкой (каждый город соединен с следующим).
- Массив
dist инициализируется так, что расстояние от города 0 до города i равно i (для начальной цепочки).
-
Обработка запросов:
- Для каждого запроса добавляется новая дорога между городами
u и v. После этого запускается BFS с города v для обновления кратчайших расстояний до всех достижимых городов.
Читать дальше →
ответить
Новый день - новая задача 2109. Adding Spaces to a String.
Условие 🧩
Дана строка s и массив индексов spaces. Нужно добавить пробелы перед символами строки, расположенными по данным индексам, и вернуть новую строку. Например, для s = "EnjoyYourCoffee" и spaces = [5, 9] результатом будет "Enjoy Your Coffee".
Если решать абы как, то можно и в ней запутаться в индексах. Мы же будем делать все максимально просто.
Идея решения 🧠
Вместо создания промежуточных строк или модификации исходной строки, мы используем построение строки с выделением памяти заранее, чтобы минимизировать накладные расходы.
Подход 🔍
- Предварительно выделяем память для результирующей строки с помощью
String::with_capacity, учитывая длину строки и количество пробелов.
- Проходим по массиву индексов spaces:
- Добавляем в результат подстроку от предыдущей позиции до текущего индекса.
- Добавляем пробел.
- После цикла добавляем оставшуюся часть строки.
- Возвращаем итоговую строку.
Анализ сложности 📊
- Временная сложность:
O(n), где n=длина строки+количество пробелов. Все операции выполняются за один проход.
- Пространственная сложность:
O(n), поскольку результирующая строка создаётся с заранее выделенной памятью.
Исходный код решения
impl Solution {
pub fn add_spaces(s: String, spaces: Vec<i32>) -> String {
let mut result = String::with_capacity(s.len() + spaces.len()); // Pre-allocate capacity for efficiency
let mut word_pos = 0;
for &space_pos in &spaces {
let space_pos = space_pos as usize; // Convert i32 to usize for indexing
result.push_str(&s[word_pos..space_pos]); // Add the substring
result.push(' '); // Add the space
word_pos = space_pos;
}
result.push_str(&s[word_pos..]); // Add the remaining substring
result
}
}
Ссылка на задачу – 1352. Product of the Last K Numbers.
📌 Описание задачи
Необходимо создать структуру ProductOfNumbers, которая:
- Позволяет добавлять числа в поток (
add(num)).
- Вычисляет произведение последних k чисел (
get_product(k)).
Гарантируется, что ответы не приведут к переполнению 32-битного целого.
💡 Идея
Будем использовать префиксные произведения.
Это позволит получать результат за O(1), выполняя деление последних значений.
Но так как деление на 0 запрещено, придётся аккуратно отслеживать этот случай и сбрасывать произведения при появлении нуля.
⚙️ Подход
- Используем
Vec<i64> для хранения префиксных произведений.
- Добавление числа:
- Если
num == 0, очищаем хранилище, так как любое произведение после нуля будет равно нулю.
- Иначе умножаем предыдущее произведение на текущее число и сохраняем результат.
- Вычисление
get_product(k):
- Если
k больше количества сохранённых чисел, возвращаем 0.
- Иначе делим последнее префиксное произведение на значение
k шагов назад.
Читать дальше →
ответить
Сегодня разберём ещё одну простую задачу 1455. Check If a Word Occurs As a Prefix of Any Word in a Sentence.
Описание задачи 📜
Дана строка sentence, состоящая из слов, разделённых пробелами, и строка searchWord. Нужно определить индекс (считаем с 1), где searchWord является префиксом какого-либо слова в sentence. Если такого слова нет — вернуть -1.
Решение 🛠️
Идея 💡
Задача сводится к простому проходу по словам строки. Мы должны проверить каждое слово: начинается ли оно с searchWord. Возвращаем индекс первого подходящего слова.
Алгоритм 🚀
- Разделяем строку
sentence на слова с помощью метода split_whitespace, который возвращает ссылки на части исходной строки.
- Проходим по словам с их индексами через
enumerate.
- Для каждого слова проверяем, начинается ли оно с
searchWord с помощью метода starts_with.
- Если находим соответствие, возвращаем индекс (преобразуем его в формат 1-based). Если совпадений нет, возвращаем
-1.
Анализ Сложности 📊
-
Временная сложность:
O(n), где n — длина строки sentence. Разделение строки и проверка префикса выполняются за линейное время.
-
Пространственная сложность:
O(k), где k — количество слов в предложении. Дополнительная память используется только для хранения указателей на слова, а не самих слов.
Исходный код решения
impl Solution {
pub fn is_prefix_of_word(sentence: String, search_word: String) -> i32 {
// Split the sentence into words using whitespace as a delimiter
let words = sentence.split_whitespace();
// Iterate through the words with their indices
for (index, word) in words.enumerate() {
// Check if search_word is a prefix of the current word
if word.starts_with(&search_word) {
return (index + 1) as i32; // Convert 1-based index to i32 and return
}
}
-1 // Return -1 if no prefix match is found
}
}
Задача второго дня Advent of Code — Red-Nosed Reports.
📘 Часть I. Описание задачи
Имеется множество отчётов, каждый из которых представляет собой последовательность целых чисел — уровней. Отчёт считается безопасным, если:
- Все уровни строго возрастают или строго убывают.
- Разность между любыми двумя соседними уровнями по модулю составляет от 1 до 3 включительно.
Пример безопасных отчётов:
Пример небезопасных отчётов:
1 2 5 9 # шаг больше 35 4 4 1 # не строго убывает
💡 Идея
Необходимо пройтись по каждой последовательности и проверить, являются ли все пары элементов:
- либо строго возрастающими (
a < b)
- либо строго убывающими (
a > b)
- и при этом |a - b| <= 3
Если хотя бы одна из этих проверок не выполняется — отчёт считается небезопасным.
Читать дальше →
ответить
Ссылка на задачу – 3174. Clear Digits.
📌 Описание задачи
Дана строка s, содержащая буквы и цифры. Из неё возможно удалять цифры только путем выполнения следующей операции:
- Удалить первую найденную цифру и ближайший нецифровой символ слева.
Вернуть итоговую строку после итеративного выполнения указанной операции до исчезновения всех цифр.
💡 Идея
Достаточно легко придумать алгоритм, формирующий ответ справа-налево (просто запоминаем, сколько символов нужно скипнуть после встреченных цифр).
Мы же реализуем решение с прямым (слева-направо) обходом строки без необходимости переворачивания результата.
- Используем буфер (
buffer) для хранения промежуточного результата.
- Используем указатель
write_index, который отслеживает место для записи следующего символа.
- При встрече цифры уменьшаем
write_index (удаляем ближайший нецифровой символ).
⚙ Подробности подхода
- Инициализируем буфер размером
s.len() (заполняем заглушками '\0').
Читать дальше →
ответить
Очередная наша задача - 3381. Maximum Subarray Sum With Length Divisible by K
Описание задачи
Дано целое число k и массив чисел nums. Необходимо найти максимальную сумму подмассива, длина которого кратна k.
🚀 Идея
Данная задача расширяет классический алгоритм нахождения максимальной суммы подмассива (алгоритм Кадане) для случаев, когда длина подмассива должна быть кратной k. Чтобы учесть это условие, мы перебираем все смещения в полуинтервале [0,k) и анализируем подмассивы с шагом k.
🔍 Подход
- Префиксные суммы:
- Вычисляем массив префиксных сумм, чтобы быстро находить сумму любого подмассива.
- Перебор смещений:
- Итерируем по всем возможным начальным смещениям
[0,k), чтобы обрабатывать подмассивы длиной, кратной k.
- Модификация алгоритма Кадане:
- Для каждого смещения применяем алгоритм нахождения максимальной суммы подмассива.
- Если текущая сумма становится отрицательной, начинаем новый расчет с текущей позиции (сброс индекса начала подмассива).
Читать дальше →
ответить
Начну-ка я минипроект по разбору ежедневных задач с LeetCode.
Решения будут на раст, ибо: модно, стильно, молодёжно!
Rust идеально подходит для задач с LeetCode благодаря высокой производительности, безопасному управлению памятью и удобным инструментам для работы с данными, обеспечивая компактный и надёжный код.
Надеюсь, такой контент будет полезен аудитории.
ответить
Ссылка на задачу — 1415. The k-th Lexicographical String of All Happy Strings of Length n.
📝 Описание задачи
"Счастливая строка" – это строка длины n, состоящая только из символов ['a', 'b', 'c'], в которой нет двух одинаковых подряд идущих символов.
Нужно найти k-ю счастливую строку в лексикографическом порядке, либо вернуть "", если таких строк меньше k.
💡 Идея
Рассмотрим связь счастливых строк с двоичными строками.
Каждая счастливая строка:
- Начинается с одного из трёх символов (
'a', 'b', 'c') → 3 варианта.
- Остальные
(n-1) символов формируются по аналогии с двоичной строкой, где у каждого символа есть ровно два возможных варианта → ×2 на каждую позицию.
Таким образом, двоичное представление k-1 почти полностью определяет структуру требуемой строки (без первого символа).
Мы можем использовать биты 0 и 1 из этого двоичного представления, чтобы выбирать между двумя допустимыми символами при итеративной генерации каждого следующего символа конкретной счастливой строки. 🚀
🔍 Детали подхода
- Определяем количество возможных строк с фиксированным первым символом:
Читать дальше →
ответить
Ссылка на задачу — 1524. Number of Sub-arrays With Odd Sum.
📌 Описание задачи
Дан массив целых чисел arr. Необходимо найти количество подмассивов с нечётной суммой.
Так как ответ может быть очень большим, его необходимо вернуть по модулю 10⁹+7.
💡 Идея
Вместо явного перебора всех подмассивов (O(N²)), можно следить за чётностью суммы префикса.
Ключевое наблюдение:
- Если текущая сумма чётная, то количество новых подмассивов с нечётной суммой равно числу префиксов с нечётной суммой.
- Если текущая сумма нечётная, то число новых подмассивов с нечётной суммой равно количеству префиксов с чётной суммой.
🛠 Детали подхода
- Следим за чётностью префиксной суммы, храня в
prefix_parity (0 - чётная, 1 - нечётная).
- Считаем количество чётных (
even_count) и нечётных (odd_count) префиксных сумм.
- Используем
fold для итеративного обновления результата.
- Добавляем соответствующие значения к result:
- Если
prefix_parity чётный, к result прибавляем odd_count.
- Если
prefix_parity нечётный, к result прибавляем even_count.
⏳ Асимптотика
- Время:
O(N) — один проход по массиву.
- Память:
O(1) — используем только несколько переменных.
💻 Исходный код
impl Solution {
pub fn num_of_subarrays(arr: Vec<i32>) -> i32 {
const MODULO: i32 = 1_000_000_007;
let (result, _, _, _) = arr.into_iter()
.fold((0, 0, 0, 1), |(result, prefix_parity, odd_count, even_count), num| {
match(prefix_parity + num) % 2 {
0 => // Even prefix → account subarrays from odd prefixes
((result + odd_count) % MODULO, 0, odd_count, even_count + 1),
_ => // Odd prefix → account subarrays from even prefixes
((result + even_count) % MODULO, 1, odd_count + 1, even_count),
}
});
result
}
}
Tags: #rust #algorithms #prefixsum
ответить
Следующая задача для разбора - 1462. Course Schedule IV
✨ Описание задачи
У нас есть numCourses курсов, пронумерованных от 0 до numCourses - 1.
Даны:
- Массив
prerequisites, где prerequisites[i] = [a, b] указывает, что курс a необходимо пройти перед курсом b.
- Массив запросов queries, где
queries[j] = [u, v] спрашивает: является ли курс u предшественником курса v.
Нужно вернуть массив булевых значений, где для каждого запроса ответ — true, если курс u является прямым или косвенным предшественником курса v; или false, если нет.
💡 Идея
Представим зависимости курсов в виде графа, где вершины — это курсы, а ребра указывают на зависимости между ними. Наша цель — определить, существует ли путь между двумя вершинами графа. Для этого можно использовать алгоритм Флойда-Уоршелла, чтобы вычислить транзитивное замыкание графа.
🛠️ Подробности подхода
- Инициализация матрицы зависимостей: Создаем булевую матрицу
n x n, где dep_matrix[i][j] обозначает, что курс i является предшественником курса j.
- Заполнение прямых зависимостей: На основе массива
prerequisites отмечаем прямые зависимости в матрице.
Читать дальше →
ответить
В нашей новой задаче - 1765. Map of Highest Peak продолжим закреплять работу с семейством простых графовых алгоритмов.
📜 Описание задачи
Вам дана матрица isWater размером m×n, где:
isWater[i][j] == 1 указывает, что клетка — это вода.isWater[i][j] == 0 указывает, что клетка — это суша.
Требуется назначить высоты каждой клетке таким образом, чтобы:
- Высота каждой клетки была неотрицательной.
- Высота любой клетки с водой была равна 0.
- Абсолютная разница высот у соседних клеток не превышала 1.
- Максимальная высота в назначенной карте была как можно больше.
💡 Идея
Мы используем поиск в ширину с несколькими источниками (multi-source BFS), начиная с клеток воды (высота 0).
На каждом шаге ближайшие клетки суши получают высоту на 1 больше текущей.
Этот метод гарантирует, что все клетки суши получают наилучшую из возможных высот, что приводит к максимизации самой высокой высоты в матрице.
🛠 Подробности подхода
- Инициализация:
- Создаём очередь и добавляем в неё все клетки воды, помечая их высотой
0.
Читать дальше →
ответить
Ссылка на задачу — 873. Length of Longest Fibonacci Subsequence.
📌 Описание задачи
Дан монотонно возрастающий массив arr. Нужно найти длину самой длинной фибоначчиевой подпоследовательности, где каждые три последовательных элемента x, y, z удовлетворяют свойству: z = x + y
Если такой подпоследовательности нет, вернуть 0.
💡 Идея
- Мы используем динамическое программирование для отслеживания самой длинной допустимой фибоначчиевой подпоследовательности для всех нетривиальных пар
(z, y), где:
x,y,z=x+y ∈ arr и x<y<z
- Рекурентное правило ДП:
dp[z,y]=dp[y,x]+1
- Для поиска подходящих
(x, y) к текущему z применяем двунаправленный итератор.
📌 Подробности метода
- Перебираем
z = arr[k], начиная с k = 2, так как нужны минимум 3 числа.
- Будем использовать два указателя (
front и back) на arr[..k]:
front движется вперёд (x увеличивается).back движется назад (y уменьшается).
- Сравниваем
x + y и z:
Читать дальше →
1 ответ
Следующая наша задача - 1014. Best Sightseeing Pair.
Описание задачи 📝
Дано: массив values, где
values[i] — это ценность туристической достопримечательности,j-i — расстояние между двумя достопримечательностями i и j.
Требуется: найти пару достопримечательностей (i < j) с максимальной совместной ценностью по формуле:
score = values[i] + values[j] + i − j
Идея 💡
Основная задача заключается в оптимизации вычислений. Если переписать формулу как:
score = (values[i] + i) + (values[j] − j),
то видно, что для эффективного решения нужно поддерживать максимум для values[j]−j во время итерации.
Это позволяет избежать вложенных циклов и сократить сложность до O(n).
Детали подхода 🛠️
- Используем обратный обход массива с помощью
.enumerate().rev().
- На каждой итерации:
- Вычисляем текущую наилучшую ценность:
score = values[i] + i + max_right,
Читать дальше →
ответить
Ссылка на задачу — 2226. Maximum Candies Allocated to K Children.
📌 Описание задачи
Дан массив candies, где candies[i] — это количество конфет в i-й куче. Нужно раздать конфеты k детям так, чтобы каждый ребёнок получил одинаковое количество конфет и все конфеты одного ребёнка были взяты из одной кучи.
Требуется найти максимальное возможное количество конфет, которое может получить каждый ребёнок.
💡 Идея
Перебор всех возможных вариантов распределения неэффективен. Вместо этого воспользуемся бинарным поиском по ответу:
- Минимальное возможное количество конфет на ребёнка —
0,
- Максимальное —
total_candies / k (тут total_candies — общее количество конфет).
Будем проверять, можно ли выдать каждому ребёнку candies_per_child конфет.
Если да, увеличиваем candies_per_child, иначе уменьшаем.
🛠 Подробности метода
- Вычисляем
total_candies — суммарное количество конфет.
- Условие быстрого выхода: если
total_candies < k, сразу возвращаем 0.
- Определяем предикат
can_share, который проверяет, можно ли распределить candies_per_child конфет на k детей.
Читать дальше →
ответить
Ссылка на задачу — 2115. Find All Possible Recipes from Given Supplies.
В этой задаче для эффективного решения важно не только выбрать эффективный алгоритм, но и аккуратно разложить строки по необходимым структурам данных, избежать лишних копирований и обеспечить ясную картину ownership'a за объектами.
📌 Описание задачи
- У нас есть список рецептов, каждому из которых соответствует список ингредиентов.
- Некоторые ингредиенты могут быть другими рецептами, а некоторые — изначально доступны (входят в список запасов).
- Нужно определить, какие рецепты можно приготовить, имея начальные запасы и возможность использовать приготовленные рецепты.
💡 Идея
Используем рекурсивный DFS для проверки доступности рецептов.
Чтобы избежать повторных вычислений, применяем мемоизацию (кеширование уже проверенных результатов).
Вместо хранения графа явным образом, мы используем индексирование рецептов и проходим по их списку ингредиентов.
🔍 Детали подхода
- Предобработка входных данных:
- Создаём хеш-таблицу для быстрого доступа к индексу каждого рецепта.
- Добавляем начальные запасы в кеш доступных ингредиентов.
Читать дальше →
ответить
Очередная задача — 2375. Construct Smallest Number From DI String сходу выглядит переборной, но может быть эффективно реализована за счёт использования графовых алгоритмов.
📝 Описание задачи
Дан строковый шаблон pattern, состоящий из символов I и D.
Необходимо построить лексикографически наименьшее число длины n+1, используя цифры от 1 до 9 без повторений, которое соответствует следующим требованиям:
'I' (увеличение) на позиции i → требует, чтобы num[i] < num[i+1].'D' (уменьшение) на позиции i → требует, чтобы num[i] > num[i+1].
💡 Идея
Рассмотрим шаблон как ориентированный граф, где каждая позиция (i) — это вершина.
- Если
pattern[i] == 'I', создаём ребро i → i+1.
- Если
pattern[i] == 'D', создаём ребро i+1 → i.
После построения графа можно выполнить топологическую сортировку, начиная с вершин с нулевой степенью захода.
Чтобы гарантировать лексикографически наименьший порядок, обрабатываем вершины через приоритетную очередь (Min-Heap).
⚙️ Детали подхода
Читать дальше →
ответить
Ссылка на задачу — 3394. Check if Grid can be Cut into Sections.
📌 Описание задачи
Дано квадратное поле n×n, в котором размещены непересекающиеся прямоугольники.
Необходимо определить, можно ли сделать две горизонтальные или две вертикальные разрезки, чтобы:
- В каждой из трёх частей оказалось хотя бы по одному прямоугольнику.
- Каждый прямоугольник остался ровно в одной части.
Если такие разрезки возможны, вернуть true, иначе — false.
Пример
- Входные данные:
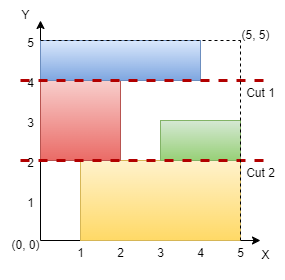
n = 5, rectangles = [[1,0,5,2],[0,2,2,4],[3,2,5,3],[0,4,4,5]]
- Ответ:
true
- Визуальное пояснение:
💡 Идея
Поскольку прямоугольники не пересекаются, возможные разрезки должны полностью разделять их на независимые группы.
Мы спроектируем прямоугольники на каждую ось. Если полученные отрезки отсортировать по координатам и просканировать их, можно определить количество неперекрывающихся сегментов, это позволит понять, возможно ли корректное разбиение.
Читать дальше →
ответить
Задача на сегодня 2381. Shifting Letters II - решается несложно, но используемая идея мне лично кажется интересной и симпатичной.
Описание задачи 🔎
Дана строка s и список операций shifts, где каждая операция задаёт начало и конец диапазона, а также направление (вперёд или назад).
Ваша задача — применить все сдвиги к строке и вернуть окончательный результат.
Идея 🔄
Для оптимизации решения и избежания повторных расчётов сдвигов, мы используем алгоритм, основанный на префиксных суммах. Это позволяет эффективно сохранять кумулятивный эффект от всех сдвигов в отдельном массиве и применять их конечному результату за один проход.
Детали решения 📝
- Создадим массив
net_shifts, где будут храниться чистые значения сдвигов для каждой позиции в строке.
- Пройдемся по всем операциям и обновим массив
net_shifts, добавляя значения в начале диапазона и вычитая их сразу после его окончания.
- Произведем один последовательный проход по строке, вычисляя кумулятивные сдвиги и применяя их для каждого символа.
Асимптотика ⏳
- Время:
O(n + m), где n — длина строки, m — количество операций.
- Память:
O(n) для массива net_shifts.
Читать дальше →
ответить
Новая задача - 689. Maximum Sum of 3 Non-Overlapping Subarrays.
Описание задачи 📜
Дано: массив чисел nums и целое число k.
Задача: найти три непересекающихся подмассива длины k с максимальной суммой и вернуть индексы их начала.
Если существует несколько решений, вернуть лексикографически минимальное.
Идея 💡
Для нахождения оптимального решения нам нужно:
- Вычислить суммы всех подмассивов длины
k с помощью техники скользящего окна.
- Найти лучшие индексы подмассивов для правой, средней и левой частей массива, используя динамическое программирование.
Это позволяет эффективно комбинировать результаты и найти оптимальное выделение трёх подмассива.
Детали подхода 🛠️
-
Скользящее окно для вычисления сумм:
- Вычисляем суммы всех подмассивов длины
k, чтобы избежать повторных расчетов.
-
Поиск лучших правых подмассивов:
- Сканируем массив справа налево, чтобы сохранить индексы подмассивов с максимальной суммой для каждого положения.
Читать дальше →
ответить
Ссылка на задачу – 2342. Max Sum of a Pair With Equal Sum of Digits
📌 Условие задачи
Дан массив положительных чисел nums. Необходимо найти максимальную сумму двух различных элементов, у которых одинаковая сумма цифр. Если таких пар нет — вернуть -1.
💡 Идея решения
Вместо хранения всех чисел с одинаковой суммой цифр, достаточно хранить только максимальное из них.
Таким образом, при встрече нового числа с такой же суммой цифр можно сразу проверять, образует ли оно лучшую пару.
🔍 Подход к решению
- Используем массив
max_per_dsum, в котором храним наибольшее число для каждой суммы цифр.
- Максимальная сумма цифр для i32 — 82, но мы ограничиваем массив сотней для простоты.
- Обрабатываем
nums за один проход, применяя функциональный стиль с filter_map:
- вычисляем сумму цифр
d_sum для числа n;
- если уже есть число с таким
d_sum, определяем текущую сумму пары и сохраняем обновлённое максимальное число;
- если это первое число с данным
d_sum, просто сохраняем его в max_per_dsum;
filter_map отбрасывает неопределённые суммы пар (None), оставляя только валидные.
Читать дальше →
ответить
Ссылка на задачу — 1028. Recover a Tree From Preorder Traversal.
📝 Описание задачи
Дано строковое представление бинарного дерева, полученное в порядке прямого обхода, где:
- Каждый узел записан в формате
Dashes + Value, где количество - (тире) указывает на глубину узла.
- Глубина корневого узла —
0, его дочерний узел имеет глубину 1, внуки — 2 и так далее.
- Если у узла есть только один ребёнок, то это всегда левый ребёнок.
Например для следующего дерева, представление будет таким: 1-2--3---4-5--6---7
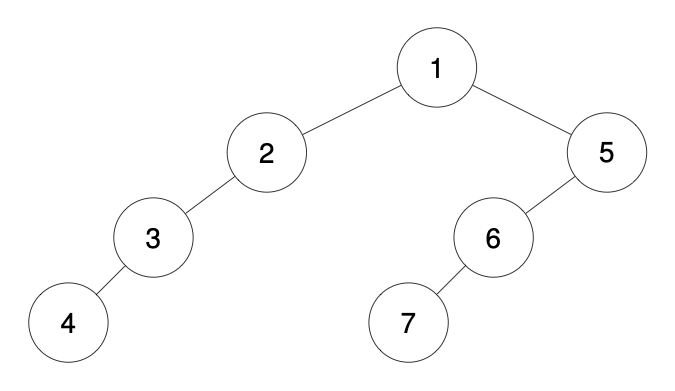
Необходимо восстановить бинарное дерево по этой строке и вернуть его корень.
💡 Идея
- Нам нужно восстановить бинарное дерево из его обхода с закодированными глубинами.
- Традиционное решение:
- разбить строку на токены (
Dashes + Value);
- затем рекурсивно собрать дерево по массиву токенов.
- Мы же сделаем чуть больше работы, и будем лениво разбирать представление на токены (вместо того, чтобы сразу сохранить их в
Vec)
Читать дальше →
ответить
Продолжаем череду задач на перебор - 1079. Letter Tile Possibilities.
📜 Описание задачи
У нас есть набор плиток, на каждой из которых напечатана одна буква, представленный в виде строки.
Необходимо подсчитать количество различных возможных непустых последовательностей букв, которые можно составить, используя плитки.
💡 Идея решения
- Будем использовать бэктрекинг.
- Чтобы избежать проверки на уникальность через
HashSet, сначала сортируем плитки, а затем группируем одинаковые плитки в сегменты.
- Далее, с помощью рекурсии, перебираем все возможные последовательности, гарантируя, что одинаковые плитки не будут использоваться более одного раза в одном наборе последовательностей.
🧑💻 Подробности подхода
- Сортировка плиток:
- Плитки сортируются для того, чтобы одинаковые плитки оказались рядом. Это позволяет нам эффективно группировать их в сегменты.
- Группировка плиток:
- Создаем массив сегментов, где каждый элемент представляет собой количество одинаковых плиток.
- Например, для строки
"AAB" сегменты будут равны [2, 1] (2 плитки "A" и 1 плитка "B").
- Бэктрекинг — для каждого сегмента мы:
- пытаемся использовать плитку (уменьшаем количество плиток в этом сегменте);
Читать дальше →
ответить
Страница
1
2
3
4
