Ссылка на задачу — 3480. Maximize Subarrays After Removing One Conflicting Pair.
📌 Описание задачи
- Дан массив чисел от
1 до n и список конфликтных пар conflicting_pairs,
где каждая пара [a, b] запрещает подотрезки[1, n] , в которых a и b встречаются совместно.
- Требуется удалить ровно одну конфликтную пару так,
чтобы получить максимальное количество подотрезков из [1, n], удовлетворяющих оставшимся ограничениям.
Пример
- Входные параметры:
n = 5, conflictingPairs = [[1,2],[2,5],[3,5]]
- Ответ:
12
- Объяснение:
Удаляем [1, 2] из массива конфликтных пар. Остаются: [[2, 5], [3, 5]].
Всего 12 подотрезков удовлетворяют условию не содержать одновременно 2 и 5 или 3 и 5.
Это отрезки: 1..1, 1..2, 1..3, 1..4, 2..2, 2..3, 2..4, 3..3, 3..4, 4..4, 4..5, 5..5
💡 Идея
- Ключевое наблюдение заключается в том, что конфликтные пары создают ограничения на диапазоны, ограничивая допустимые подотрезки.
Читать дальше →
ответить
Ссылка на задачу — 2226. Maximum Candies Allocated to K Children.
📌 Описание задачи
Дан массив candies, где candies[i] — это количество конфет в i-й куче. Нужно раздать конфеты k детям так, чтобы каждый ребёнок получил одинаковое количество конфет и все конфеты одного ребёнка были взяты из одной кучи.
Требуется найти максимальное возможное количество конфет, которое может получить каждый ребёнок.
💡 Идея
Перебор всех возможных вариантов распределения неэффективен. Вместо этого воспользуемся бинарным поиском по ответу:
- Минимальное возможное количество конфет на ребёнка —
0,
- Максимальное —
total_candies / k (тут total_candies — общее количество конфет).
Будем проверять, можно ли выдать каждому ребёнку candies_per_child конфет.
Если да, увеличиваем candies_per_child, иначе уменьшаем.
🛠 Подробности метода
- Вычисляем
total_candies — суммарное количество конфет.
- Условие быстрого выхода: если
total_candies < k, сразу возвращаем 0.
- Определяем предикат
can_share, который проверяет, можно ли распределить candies_per_child конфет на k детей.
Читать дальше →
ответить
Ссылка на задачу — 3356. Zero Array Transformation II.
📝 Описание задачи
Дан массив nums длины N и список запросов queries, каждый из которых задаётся как [li, ri, vali]. Запрос означает, что значения в диапазоне [li, ri] можно уменьшить на любое число от 0 до vali независимо друг от друга.
Нужно найти минимальное число первых запросов k, после которых nums может превратится в массив, состоящий только из нулей. Если это невозможно — вернуть -1.
💡 Идея
Вместо того, чтобы изменять nums напрямую, будем хранить массив последовательных изменений к декременту (updates). Он позволяет эффективно применять диапазонные операции без лишних вычислений.
Чтобы минимизировать количество обработанных запросов, будем использовать жадную стратегию обработки запросов:
- Обрабатываем
nums последовательно
- Для каждой позиции
i, если nums[i] ещё не стал 0, пытаемся применить минимально возможное число новых запросов из списка.
⚙️ Детали подхода
- Используем массив
updates (N+1 элементов), где updates[i] хранит последовательные изменения к декременту значений.
Читать дальше →
ответить
Ссылка на задачу — 3479. Fruits Into Baskets III.
📌 Описание задачи
У нас есть два массива:
fruits[i] — количество фруктов i-го типаbaskets[j] — вместимость j-й корзины
Нужно распределить фрукты по корзинам слева направо по следующим правилам:
- Каждый тип фруктов должен быть помещён в самую левую подходящую корзину,
где вместимость соответствует (≥) количеству этих фруктов.
- Одна корзина может содержать только один тип фруктов.
- Если фрукт не удалось разместить — он остаётся неразмещённым.
Требуется вернуть количество неразмещённых фруктов.
💡 Идея
Используем дерево отрезков для эффективного поиска первой подходящей корзины.
Это позволит быстро находить и обновлять вместимость корзин за логарифмическое время, что намного быстрее наивного перебора.
🔍 Подробности подхода
- Построение дерева отрезков 🌳:
- Создаём дерево отрезков для максимумов на интервалах, инициализируюя его вместимостями корзин.
Читать дальше →
ответить
Ссылка на задачу — 3306. Count of Substrings Containing Every Vowel and K Consonants II.
📌 Условие задачи
Дана строка word и неотрицательное число k.
Необходимо подсчитать количество подстрок, в которых встречаются все гласные буквы ('a', 'e', 'i', 'o', 'u') хотя бы по одному разу и ровно k согласных.
💡 Идея
Будем использовать подход «скользящего окна», отслеживая позиции последних появлений гласных и согласных букв.
Это позволяет эффективно перемещать границы окна и быстро проверять условия задачи при изменении количества согласных и наличии всех гласных.
🛠️ Детали подхода
- Для каждой гласной буквы сохраняется её последняя позиция.
- Для согласных используется итератор, последовательно предоставляющий позиции согласных в строке.
- Если количество согласных становится больше
k, левая граница окна перемещается вперёд.
- При каждом совпадении условий (ровно
k согласных и присутствуют все гласные) подсчитывается количество допустимых подстрок.
⏳ Асимптотика
Читать дальше →
ответить
Ссылка на задачу — 2379. Minimum Recolors to Get K Consecutive Black Blocks.
📌 Описание задачи
Дана строка blocks, состоящая из символов 'W' (белый) и 'B' (чёрный).
Необходимо определить минимальное число перекрашиваний белых блоков в чёрные, чтобы получить хотя бы одну последовательность из k подряд идущих чёрных блоков.
💡 Идея
Используем технику скользящего окна:
- будем двигать окно размера
k по строке и считать количество белых блоков внутри окна;
- минимальное количество белых блоков среди всех окон и будет ответом.
📖 Детали подхода
- Посчитаем число белых блоков в первом окне размера
k.
- Сдвигаем окно вправо на один символ за раз:
- если символ, который «входит» в окно, белый (
'W'), увеличиваем счётчик;
- если символ, который «выходит» из окна, белый, уменьшаем счётчик.
- После каждого сдвига окна обновляем минимальное найденное значение.
- Итоговый ответ — это минимальное число белых блоков за всё время обхода.
⏳ Асимптотика
- Время:
O(n) — каждый символ просматривается не более двух раз.
- Память:
O(1) — используется константная дополнительная память.
🛠️ Исходный код
impl Solution {
pub fn minimum_recolors(blocks: String, k: i32) -> i32 {
let blocks = blocks.as_bytes();
let k = k as usize;
// Count white blocks ('W') in the first window of size k
let initial_recolors = blocks[..k].iter().filter(|&&b| b == b'W').count() as i32;
// Slide window over the blocks using iterator methods
blocks
.windows(k+1)
.fold((initial_recolors, initial_recolors), |(current, min), window| {
// Update recolors based on outgoing and incoming blocks
let next = current
+ (window.last() == Some(&b'W')) as i32
- (window.first() == Some(&b'W')) as i32;
(next, min.min(next))
}).1
}
}
Tags: #rust #algorithms #counting
ответить
Очередная наша задача — 2579. Count Total Number of Colored Cells, как ни странно, красиво решается на шахматной доске ☺.
📜 Описание задачи
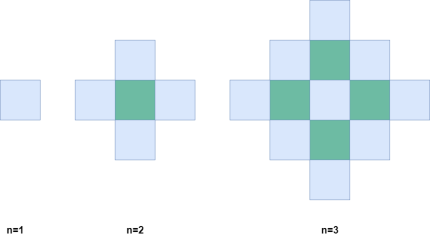
Дана бесконечная двумерная сетка с неокрашенными клетками. В течение n минут выполняются следующие действия:
- В первую минуту любая клетка окрашивается в синий цвет.
- В каждую следующую минуту закрашиваются все неокрашенные клетки, имеющие общую сторону с уже окрашенными.
Необходимо вычислить количество окрашенных клеток после n минут.
🧠 Идея
Если рассмотреть процесс закрашивания клеток на шахматной доске, можно увидеть, что в момент n окрашенные клетки образуют два наложенных квадрата:
- Квадрат размером
n × n
- Квадрат размером
(n-1) × (n-1)
Сумма площадей этих двух квадратов и дает общее количество окрашенных клеток.
🚀 Детали подхода
✅ Применяем формулу: Total = n²+(n−1)²
⏳ Асимптотика
- Временная сложность:
O(1)
(мгновенный расчет по формуле)
- Пространственная сложность:
O(1)
(используется только переменная n)
💻 Исходный код
impl Solution {
pub fn colored_cells(n: i32) -> i64 {
let n = n as i64;
n*n + (n-1)*(n-1)
}
}
Tags: #rust #algorithms #math
ответить
Ссылка на задачу - 1780. Check if Number is a Sum of Powers of Three.
📌 Описание задачи
Дано число n. Нужно определить, можно ли представить его в виде суммы различных степеней тройки.
🔹 Пример:
- 📥 Ввод:
n = 12
- 📤 Вывод:
true
- 💡 Объяснение:
12 = 3⁰+3¹+3² = 1 + 3 + 9.
💡 Идея
Рассмотрим представление n в троичной системе счисления:
- Если в записи числа есть цифра
2, то решения нет (так как нельзя взять две одинаковые степени).
- Если в записи есть только
0 и 1, то решение существует (мы просто берём соответствующие степени тройки).
Таким образом, задача сводится к поразрядной проверке числа в троичной системе счисления.
🚀 Детали подхода
Будем использовать рекурсию и деление числа на 3:
- База рекурсии: Если
n == 0, то мы успешно разложили число, возвращаем true.
- Шаг рекурсии: Если
n % 3 == 2, то n нельзя разложить, возвращаем false.
- Рекурсивный вызов: Проверяем
n / 3, повторяя процесс.
⏱ Асимптотика
- Временная сложность:
O(log n), так как n уменьшается в 3 раза за итерацию.
- Пространственная сложность:
O(log n) из-за глубины рекурсии
(несложно алгоритм преобразовать в цикл, чтобы получить O(1)).
📝 Исходный код
impl Solution {
pub fn check_powers_of_three(n: i32) -> bool {
n == 0 || (n % 3 != 2 && Self::check_powers_of_three(n / 3))
}
}
Tags: #rust #algorithms #math
ответить
Ссылка на задачу - 2161. Partition Array According to Given Pivot.
В данной задаче нам предстоит реализовать базовую подзадачу Быстрой сортировки, но с дополнительным требованием сохранения относительного порядка, отчего стандартные методы реализации Q-sort нас не будут устраивать ☹
📌 Описание задачи
Дан массив nums и число pivot. Требуется переставить элементы массива так, чтобы:
- Все элементы меньше
pivot шли первыми.
- Все элементы равные
pivot находились в середине.
- Все элементы больше
pivot шли в конце.
- Относительный порядок элементов в каждой группе сохранялся.
💡 Идея
Мы хотим разделить массив на три части, не создавая лишние структуры данных.
Вместо этого заполним результирующий вектор напрямую, обрабатывая массив в три прохода.
🛠️ Детали подхода
1️⃣ Первый проход: добавляем в результат все элементы < pivot.
2️⃣ Подсчет и второй проход: вычисляем количество вхождений pivot в массиве и добавляем pivot в результат pivot_count раз.
3️⃣ Третий проход: добавляем все элементы > pivot в результат.
Используем Vec::with_capacity(nums.len()), чтобы избежать лишних аллокаций.
📊 Асимптотика
- Временная сложность:
O(n) — три прохода по nums.
- Дополнительная память:
O(1) — все данные хранятся только в результирующем массиве
(который всё же имеет размер O(n)).
💻 Исходный код
impl Solution {
pub fn pivot_array(nums: Vec<i32>, pivot: i32) -> Vec<i32> {
let mut result = Vec::with_capacity(nums.len());
// First pass: Collect elements smaller than pivot
result.extend(nums.iter().filter(|&&num| num < pivot));
// Count occurrences of pivot
let pivot_count = nums.iter().filter(|&&num| num == pivot).count();
// Insert pivot elements
result.extend(std::iter::repeat(pivot).take(pivot_count));
// Third pass: Collect elements greater than pivot using into_iter() to take ownership
result.extend(nums.into_iter().filter(|&num| num > pivot));
result
}
}
Tags: #rust #algorithms
1 ответ
Ссылка на задачу - 2570. Merge Two 2D Arrays by Summing Values.
📌 Описание задачи
Даны два отсортированных списка nums1 и nums2, где каждый элемент представлен в виде [id, value].
Нужно объединить их в один список, упорядоченный по id, при этом суммируя значения для совпадающих id.
💡 Идея
Так как оба списка уже отсортированы по id, можно пройтись по ним одновременно, сравнивая id и добавляя элементы в результат.
Такой метод позволяет решить задачу за O(n + m) без дополнительной сортировки.
🛠 Подробности подхода
- Используем два индекса
i и j для итерации по nums1 и nums2.
- Сравниваем текущие
id:
- Если
id1 < id2 → добавляем nums1[i] в результат, сдвигаем i.
- Если
id1 > id2 → добавляем nums2[j] в результат, сдвигаем j.
- Если
id1 == id2 → суммируем значения, добавляем результат, сдвигаем оба указателя.
- Добавляем оставшиеся элементы из
nums1 и nums2, если таковые имеются.
Читать дальше →
ответить
Ссылка на задачу — 2460. Apply Operations to an Array.
📝 Описание задачи
Дан массив nums, состоящий из неотрицательных целых чисел. Нужно последовательно выполнить следующие операции:
- Для каждого валидного
i (в порядке возрастания):
- eсли
nums[i] == nums[i + 1], удвоить nums[i] и заменить nums[i + 1] на 0.
- После всех операций сдвинуть все нули в конец массива, сохраняя порядок оставшихся чисел.
- Вернуть изменённый массив.
💡 Идея
Решение можно выполнить за один проход, используя два указателя (read и write):
- Читаем массив и объединяем соседние одинаковые элементы.
- Перемещаем ненулевые элементы в начало массива.
- Оставшиеся ячейки заполняем нулями.
Такой подход позволяет изменять массив на месте, не используя дополнительную память.
📌 Детали подхода
- Используем два указателя (
read и write):
read проходит по массиву.write отслеживает следующую позицию для ненулевых чисел.
Читать дальше →
ответить
Ссылка на задачу — 873. Length of Longest Fibonacci Subsequence.
📌 Описание задачи
Дан монотонно возрастающий массив arr. Нужно найти длину самой длинной фибоначчиевой подпоследовательности, где каждые три последовательных элемента x, y, z удовлетворяют свойству: z = x + y
Если такой подпоследовательности нет, вернуть 0.
💡 Идея
- Мы используем динамическое программирование для отслеживания самой длинной допустимой фибоначчиевой подпоследовательности для всех нетривиальных пар
(z, y), где:
x,y,z=x+y ∈ arr и x<y<z
- Рекурентное правило ДП:
dp[z,y]=dp[y,x]+1
- Для поиска подходящих
(x, y) к текущему z применяем двунаправленный итератор.
📌 Подробности метода
- Перебираем
z = arr[k], начиная с k = 2, так как нужны минимум 3 числа.
- Будем использовать два указателя (
front и back) на arr[..k]:
front движется вперёд (x увеличивается).back движется назад (y уменьшается).
- Сравниваем
x + y и z:
Читать дальше →
1 ответ
Ссылка на задачу — 1524. Number of Sub-arrays With Odd Sum.
📌 Описание задачи
Дан массив целых чисел arr. Необходимо найти количество подмассивов с нечётной суммой.
Так как ответ может быть очень большим, его необходимо вернуть по модулю 10⁹+7.
💡 Идея
Вместо явного перебора всех подмассивов (O(N²)), можно следить за чётностью суммы префикса.
Ключевое наблюдение:
- Если текущая сумма чётная, то количество новых подмассивов с нечётной суммой равно числу префиксов с нечётной суммой.
- Если текущая сумма нечётная, то число новых подмассивов с нечётной суммой равно количеству префиксов с чётной суммой.
🛠 Детали подхода
- Следим за чётностью префиксной суммы, храня в
prefix_parity (0 - чётная, 1 - нечётная).
- Считаем количество чётных (
even_count) и нечётных (odd_count) префиксных сумм.
- Используем
fold для итеративного обновления результата.
- Добавляем соответствующие значения к result:
- Если
prefix_parity чётный, к result прибавляем odd_count.
- Если
prefix_parity нечётный, к result прибавляем even_count.
⏳ Асимптотика
- Время:
O(N) — один проход по массиву.
- Память:
O(1) — используем только несколько переменных.
💻 Исходный код
impl Solution {
pub fn num_of_subarrays(arr: Vec<i32>) -> i32 {
const MODULO: i32 = 1_000_000_007;
let (result, _, _, _) = arr.into_iter()
.fold((0, 0, 0, 1), |(result, prefix_parity, odd_count, even_count), num| {
match(prefix_parity + num) % 2 {
0 => // Even prefix → account subarrays from odd prefixes
((result + odd_count) % MODULO, 0, odd_count, even_count + 1),
_ => // Odd prefix → account subarrays from even prefixes
((result + even_count) % MODULO, 1, odd_count + 1, even_count),
}
});
result
}
}
Tags: #rust #algorithms #prefixsum
ответить
Ссылка на задачу — 2467. Most Profitable Path in a Tree.
📌 Описание задачи
Дано неориентированное корневое дерево с n узлами (нумерованными от 0 до n-1).
- У каждого узла есть врата, открытие которых может принести прибыль или потребовать затрат (
amount[i]).
- Алиса начинает движение от корня (
0) к какому-либо листу, выбирая максимально выгодный путь.
- Боб начинает движение из указанной вершины
bob и движется к корню (0).
- Если Алиса и Боб одновременно посещают узел, они делят
стоимость/прибыль пополам.
Нужно найти максимальный чистый доход Алисы при оптимальном выборе пути.
💭 Идея
Вместо раздельного запуска BFS для поиска пути Боба и последующего прохода динамического программирования по узлам дерева, мы решим задачу одним рекурсивным DFS-проходом.
Для каждого узла будем вычислять:
alice_profit[node] – максимальный доход, который может собрать Алиса из поддерева.bob_distance[node] – расстояние на пути Боба до этой вершины.- Если Боб раньше доберётся до узла → Алиса ничего не получит.
Читать дальше →
ответить
Ссылка на задачу — 889. Construct Binary Tree from Preorder and Postorder Traversal.
📌 Описание задачи
Нам даны прямой (preorder) и обратный (postorder) обходы бинарного дерева.
Необходимо восстановить дерево по этим обходам.
Основные свойства обходов:
- Preorder (прямой обход):
[корень → левый → правый]
- Postorder (обратный обход):
[левый → правый → корень]
💡 Идея
Для построения дерева используем рекурсивный подход, основанный на двух ключевых наблюдениях:
- 1️⃣ Каждый новый узел получает значение из
preorder
→ так мы всегда сначала создаем корень поддерева.
- 2️⃣ Поддерево считается полностью построенным, когда его значение встречается в
postorder
→ это сигнал к завершению рекурсии.
🔍 Детали подхода
- Используем итераторы
Peekable<Iterator> для эффективного прохода по preorder и postorder.
- Берем значение из
preorder и создаем новый узел.
- Рекурсивно создаем левое поддерево, если
postorder пока не указывает на текущий корень.
Читать дальше →
ответить
Ссылка на задачу — 1028. Recover a Tree From Preorder Traversal.
📝 Описание задачи
Дано строковое представление бинарного дерева, полученное в порядке прямого обхода, где:
- Каждый узел записан в формате
Dashes + Value, где количество - (тире) указывает на глубину узла.
- Глубина корневого узла —
0, его дочерний узел имеет глубину 1, внуки — 2 и так далее.
- Если у узла есть только один ребёнок, то это всегда левый ребёнок.
Например для следующего дерева, представление будет таким: 1-2--3---4-5--6---7
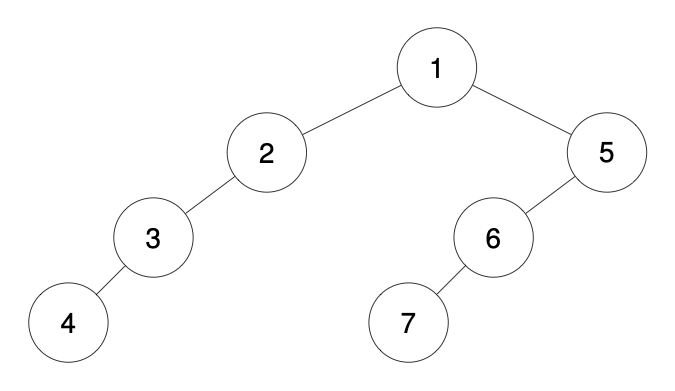
Необходимо восстановить бинарное дерево по этой строке и вернуть его корень.
💡 Идея
- Нам нужно восстановить бинарное дерево из его обхода с закодированными глубинами.
- Традиционное решение:
- разбить строку на токены (
Dashes + Value);
- затем рекурсивно собрать дерево по массиву токенов.
- Мы же сделаем чуть больше работы, и будем лениво разбирать представление на токены (вместо того, чтобы сразу сохранить их в
Vec)
Читать дальше →
ответить
Ссылка на задачу – 1261. Find Elements in a Contaminated Binary Tree.
📝 Описание задачи
Дано двоичное дерево, в котором:
- Корень всегда имеет значение
0.
- Для каждого узла со значением
x:
- Если есть левый потомок, то его значение
2 * x + 1.
- Если есть правый потомок, то его значение
2 * x + 2.
Значения всех узлов загрязнены (-1).
Нужно реализовать структуру FindElements, которая:
- Принимает корень «загрязнённого» дерева в конструкторе.
- Реализует
find(target) — метод, проверяющий существует ли узел с таким значением.
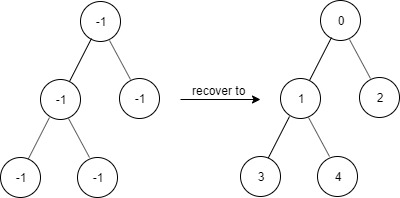
💡 Идея
Восстанавливать дерево не требуется!
Вместо этого мы вычисляем путь к узлу target, определяя его родителя и положение.
🔍 Детали подхода
- Поиск родителя (
parent):
Читать дальше →
ответить
Ссылка на задачу — 2523. Closest Prime Numbers in Range.
📌 Описание задачи
Нам даны два целых числа left и right.
Нужно найти два ближайших простых числа num1 и num2 таких, что:
left ≤ num1 < num2 ≤ right- Оба числа простые
- Разница
num2 - num1 минимальна среди всех возможных пар
Если существует несколько пар с одинаковой разницей, выбрать пару с меньшим первым числом.
Если таких чисел нет, вернуть [-1, -1].
🧠 Идея
Будем просто итерироваться по парам соседних простых чисел в заданом диапазоне.
Но, так как простые близнецы (пары простых чисел, разница между которыми равна 2) встречаются довольно часто (их плотность примерно 1 / log²(n)) мы можем эффективно ввести условие раннего выхода, которое значительно улучшает среднюю производительность алгоритма.
🔍 Подход
- Обработка граничных случаев:
- Если
left ≤ 2 и right ≥ 3, сразу возвращаем [2, 3].
- Перебор чисел в диапазоне:
- Проверяем каждое число на простоту с помощью
is_prime(n), работающей за O(√n).
Читать дальше →
ответить
Ссылка на задачу — 1980. Find Unique Binary String.
Кайфовая задачка для тех, кто не прогуливал лекции по мат. анализу ☺
📌 Описание задачи
Дан массив nums, содержащий n различных бинарных строк длины n.
Необходимо найти любую бинарную строку длины n, которая не содержится в nums.
💡 Идея
Используем диагонализацию Кантора:
- Если пройти по диагонали массива строк и инвертировать каждый символ (
'0' → '1', '1' → '0'), то полученная строка гарантированно отличается от каждой строки в nums хотя бы в одном символе.
- Это означает, что такая строка не может присутствовать в
nums.
🔍 Подробности подхода
- Итерируемся по индексам
0..n.
- Берем
i-й символ i-й строки.
- Инвертируем его (
'0' → '1', '1' → '0').
- Собираем новые символы в строку и возвращаем её.
📊 Асимптотика
- Временная сложность:
O(n) — один проход по n элементам.
- Дополнительная память:
O(n) — единственное, что создаётся, это строка длины n.
Визуальный пример
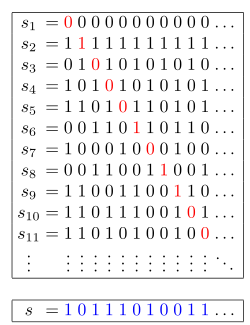
🦀 Исходный код
impl Solution {
pub fn find_different_binary_string(nums: Vec<String>) -> String {
let n = nums.len();
// Generate a new binary string by flipping the diagonal elements.
(0..n)
.map(|i| Self::inverse_char(nums[i].as_bytes()[i] as char))
.collect()
}
fn inverse_char(c: char) -> char {
match c {
'0' => '1',
'1' => '0',
_ => unreachable!("Unexpected character: {}", c),
}
}
}
Tags: #rust #algorithms #math
ответить
Ссылка на задачу — 2965. Find Missing and Repeated Values.
📌 Описание задачи
Дан n×n целочисленный массив grid, содержащий числа от 1 до n².
Одно число повторяется дважды (a), а одно отсутствует (b).
Нужно найти их.
💡 Идея
Мы можем использовать математические свойства сумм чисел:
Разница между ожидаемыми и фактическими значениями позволит выразить a и b через систему уравнений.
🚀 Детали подхода
- Вычисляем ожидаемую сумму и ожидаемую сумму квадратов для чисел от
1 до n².
- Проходим по
grid, вычисляя фактическую сумму и фактическую сумму квадратов.
- Находим промежуточные величины для системы уравнений:
Читать дальше →
ответить
Ссылка на задачу — 1415. The k-th Lexicographical String of All Happy Strings of Length n.
📝 Описание задачи
"Счастливая строка" – это строка длины n, состоящая только из символов ['a', 'b', 'c'], в которой нет двух одинаковых подряд идущих символов.
Нужно найти k-ю счастливую строку в лексикографическом порядке, либо вернуть "", если таких строк меньше k.
💡 Идея
Рассмотрим связь счастливых строк с двоичными строками.
Каждая счастливая строка:
- Начинается с одного из трёх символов (
'a', 'b', 'c') → 3 варианта.
- Остальные
(n-1) символов формируются по аналогии с двоичной строкой, где у каждого символа есть ровно два возможных варианта → ×2 на каждую позицию.
Таким образом, двоичное представление k-1 почти полностью определяет структуру требуемой строки (без первого символа).
Мы можем использовать биты 0 и 1 из этого двоичного представления, чтобы выбирать между двумя допустимыми символами при итеративной генерации каждого следующего символа конкретной счастливой строки. 🚀
🔍 Детали подхода
- Определяем количество возможных строк с фиксированным первым символом:
Читать дальше →
ответить
Очередная задача — 2375. Construct Smallest Number From DI String сходу выглядит переборной, но может быть эффективно реализована за счёт использования графовых алгоритмов.
📝 Описание задачи
Дан строковый шаблон pattern, состоящий из символов I и D.
Необходимо построить лексикографически наименьшее число длины n+1, используя цифры от 1 до 9 без повторений, которое соответствует следующим требованиям:
'I' (увеличение) на позиции i → требует, чтобы num[i] < num[i+1].'D' (уменьшение) на позиции i → требует, чтобы num[i] > num[i+1].
💡 Идея
Рассмотрим шаблон как ориентированный граф, где каждая позиция (i) — это вершина.
- Если
pattern[i] == 'I', создаём ребро i → i+1.
- Если
pattern[i] == 'D', создаём ребро i+1 → i.
После построения графа можно выполнить топологическую сортировку, начиная с вершин с нулевой степенью захода.
Чтобы гарантировать лексикографически наименьший порядок, обрабатываем вершины через приоритетную очередь (Min-Heap).
⚙️ Детали подхода
Читать дальше →
ответить
Продолжаем череду задач на перебор - 1079. Letter Tile Possibilities.
📜 Описание задачи
У нас есть набор плиток, на каждой из которых напечатана одна буква, представленный в виде строки.
Необходимо подсчитать количество различных возможных непустых последовательностей букв, которые можно составить, используя плитки.
💡 Идея решения
- Будем использовать бэктрекинг.
- Чтобы избежать проверки на уникальность через
HashSet, сначала сортируем плитки, а затем группируем одинаковые плитки в сегменты.
- Далее, с помощью рекурсии, перебираем все возможные последовательности, гарантируя, что одинаковые плитки не будут использоваться более одного раза в одном наборе последовательностей.
🧑💻 Подробности подхода
- Сортировка плиток:
- Плитки сортируются для того, чтобы одинаковые плитки оказались рядом. Это позволяет нам эффективно группировать их в сегменты.
- Группировка плиток:
- Создаем массив сегментов, где каждый элемент представляет собой количество одинаковых плиток.
- Например, для строки
"AAB" сегменты будут равны [2, 1] (2 плитки "A" и 1 плитка "B").
- Бэктрекинг — для каждого сегмента мы:
- пытаемся использовать плитку (уменьшаем количество плиток в этом сегменте);
Читать дальше →
ответить
Ссылка на задачу – 1718. Construct the Lexicographically Largest Valid Sequence.
📌 Условие задачи
Дано число n. Необходимо построить последовательность, удовлетворяющую следующим условиям:
- Число
1 встречается ровно один раз.
- Каждое число
i от 2 до n встречается ровно дважды.
- Для каждого числа
i > 1, два его вхождения в последовательность находятся на расстоянии ровно i.
- Среди всех возможных последовательностей требуется выбрать лексикографически наибольшую.
💡 Идея
Бэктрекинг — хороший способ решения данной задачи.
Чтобы получить лексикографически наибольшую последовательность, мы должны размещать сначала наибольшие числа.
🔄 Подробности метода
- Рекурсивно заполняем последовательность, начиная с первого свободного индекса.
- Используем массив
used, который отслеживает, какие числа уже размещены.
- Пропускаем занятые позиции.
- Проверяем возможность размещения числа заранее, прежде чем выполнять рекурсию.
Читать дальше →
ответить
Ссылка на задачу – 1352. Product of the Last K Numbers.
📌 Описание задачи
Необходимо создать структуру ProductOfNumbers, которая:
- Позволяет добавлять числа в поток (
add(num)).
- Вычисляет произведение последних k чисел (
get_product(k)).
Гарантируется, что ответы не приведут к переполнению 32-битного целого.
💡 Идея
Будем использовать префиксные произведения.
Это позволит получать результат за O(1), выполняя деление последних значений.
Но так как деление на 0 запрещено, придётся аккуратно отслеживать этот случай и сбрасывать произведения при появлении нуля.
⚙️ Подход
- Используем
Vec<i64> для хранения префиксных произведений.
- Добавление числа:
- Если
num == 0, очищаем хранилище, так как любое произведение после нуля будет равно нулю.
- Иначе умножаем предыдущее произведение на текущее число и сохраняем результат.
- Вычисление
get_product(k):
- Если
k больше количества сохранённых чисел, возвращаем 0.
- Иначе делим последнее префиксное произведение на значение
k шагов назад.
Читать дальше →
ответить
Страница
1
2
3
