С нами с 26-11-2024
Карма: 469
Постов: 113
Комментариев: 24
Регулярно выкладываю разборы LeetCode задач с реализацией на Rust.
Задача 9 дня Advent of Code — Disk Fragmenter.
😊 Часть I. Описание задачи
На диске из N секторов хранятся файлы, каждый занимая непрерывный блок секторов. Между блоками могут быть «пробелы» (свободные сектора).
- Задача: последовательно перемещать по одному сектору каждого файла (начиная с конца списка) в самый левый доступный свободный сектор, пока не исчезнут все разрывы.
- Пример:
В начале: 00...111...2...333.44.5555.6666.777.888899После: 0099811188827773336446555566..............
😊 Часть II. Описание задачи
Теперь вместо по-секторного перемещения перемещаем файлы целиком, один раз для каждого файла, в порядке убывания file_id. Для каждого файла (перебираем справа-налево) ищем самый левый свободный диапазон длины ≥ размера файла;
если он находится левее текущего — перемещаем файл, иначе оставляем на месте.
- Пример:
В начале: 00...111...2...333.44.5555.6666.777.888899После: 00992111777.44.333....5555.6666.....8888..
💡 Идея решения
Строим дерево отрезков над массивом из N секторов.
Читать дальше →
ответить
Ссылка на задачу с LeetCode — 2444. Count Subarrays With Fixed Bounds.
📋 Условие задачи
- Дан массив целых чисел
nums и два целых числа minK и maxK.
- Необходимо посчитать количество подотрезков (непрерывных подмассивов), в которых минимальный элемент равен
minK, а максимальный — maxK.
Пример:
- Ввод:
nums = [1,3,5,2,7,5], minK = 1, maxK = 5
- Вывод:
2
- Пояснение: Подходящие подотрезки — [1,3,5] и [1,3,5,2].
💡 Идея
- Элементы, выходящие за пределы
[minK, maxK], ломают возможность создать валидный подотрезок.
- Поэтому нужно работать только с кусками массива, где все элементы находятся внутри заданных границ.
- В каждом таком куске мы будем отслеживать последние появления
minK и maxK и считать количество возможных подотрезков на лету.
🛠️ Детали подхода
- Разбиваем массив на куски (
chunk_by), где элементы либо все в пределах [minK, maxK], либо все вне.
- Для каждого валидного куска (на каждой позиции):
- Запоминаем последние индексы появления
minK и maxK.
Читать дальше →
ответить
Задача 8-го дня Advent of Code — Resonant Collinearity.
🧩 Часть I. Условие задачи
В городе расставлены антенны, каждая из которых настроена на определённую частоту, обозначенную символом (a–z,A–Z,0–9). Если две антенны одной частоты расположены на прямой, и одна из них находится ровно в два раза дальше от точки, чем другая, то в этой точке возникает антинод.
Нужно найти количество уникальных позиций на карте, в которых возникает антинод. Позиции должны лежать в пределах карты. Антенны с разными частотами не создают антиноду.
💡 Идея
Для каждой частоты рассматриваем все пары антенн, стоящих на одной частоте. Каждая пара порождает ровно два симметричных антинода, расположенных по формуле:
(2*r0 - r1, 2*c0 - c1) и (2*r1 - r0, 2*c1 - c0)
Затем добавляем эти позиции в хеш-сет, если они находятся в пределах границ карты.
🧩 Часть II. Условие задачи
Читать дальше →
ответить
Ссылка на задачу с LeetCode — 2338. Count the Number of Ideal Arrays.
📋 Описание задачи
Дан массив длины n, состоящий из целых чисел от 1 до maxValue. Массив называется «идеальным», если:
- Каждый элемент принадлежит диапазону
[1, maxValue]
- Каждый следующий элемент делится на предыдущий
Нужно посчитать количество различных идеальных массивов длины n.
Ответ вернуть по модулю 10⁹ + 7.
💬 Пример
- Вход:
n = 2, maxValue = 5
- Выход:
10
- Пояснение: Возможные идеальные массивы:
- Начинаются с
1 (5 массивов): [1,1], [1,2], [1,3], [1,4], [1,5]
- Начинаются с
2 (2 массива): [2,2], [2,4]
- Начинаются с
3 (1 массив): [3,3]
- Начинаются с
4 (1 массив): [4,4]
- Начинаются с
5 (1 массив): [5,5]
- Всего:
5 + 2 + 1 + 1 + 1 = 10 идеальных массивов.
💡 Идея
- Любую цепочку
i₀ → i₁ → ... → iₙ можно поделить на i₀, сведя задачу к подсчёту цепочек, начинающихся с единицы:
Читать дальше →
ответить
Задача 7-го дня Advent of Code — Bridge Repair.
📘 Часть I. Условие задачи
У инженеров почти готова калибровка оборудования, но из формул пропали все операторы!
Остались только числа. В каждой строке входных данных указано:
- Слева — целевое значение;
- Справа — последовательность чисел.
Задача: вставить между числами операторы + и *, чтобы получить целевое значение.
Важно: выражения вычисляются строго слева направо, без учёта приоритетов операций.
Например:
190: 10 19
3267: 81 40 27
Требуется определить, какие строки могут быть истинными, и посчитать сумму их целевых значений.
💡 Идея
- Каждую строку можно представить как выражение, в которое надо вставить операторы.
- Количество вставок —
len(seq) - 1.
- Для каждой строки мы перебираем все возможные комбинации из операторов
+ и * и проверяем, приводит ли результат к целевому числу.
Так как порядок чисел менять нельзя и вычисления всегда происходят слева направо, задача хорошо ложится на рекурсивный перебор (бэктрекинг).
Читать дальше →
ответить
Задача 6-го дня Advent of Code — Guard Gallivant.
📘 Часть I. Описание задачи
Нам требуется смоделировать движение охранника по лаборатории, представленной в виде сетки.
- Охранник начинает в определённой клетке, смотрит в одном из четырёх направлений и следует следующим правилам:
- Если перед ним препятствие (
#), он поворачивает направо на 90°.
- Иначе делает шаг вперёд.
Задача — определить количество уникальных клеток, которые охранник посетит, прежде чем покинет карту.
💡 Идея
Необходимо симулировать движение охранника, учитывая его текущую позицию и направление. Для отслеживания посещённых клеток используется двумерный массив, где каждая клетка хранит информацию о направлениях, с которых она была посещена. Если охранник возвращается в ту же клетку с тем же направлением, это означает начало цикла.
📘 Часть II. Описание задачи
Во второй части задачи требуется определить количество позиций, где добавление одного нового препятствия приведёт к тому, что охранник зациклится и никогда не покинет карту. Очевидно, что нельзя размещать препятствие в начальной позиции охранника.
💡 Идея
Читать дальше →
ответить
Задача пятого дня Advent of Code - Print Queue.
📘 Часть I. Условие задачи
- Набор страниц необходимо печатать в определённом порядке.
- Каждое правило задаётся в виде
X | Y, что означает: если обе страницы X и Y присутствуют в обновлении, то X должна появиться раньше Y.
- Дан список правил и набор последовательностей страниц.
- Требуется найти те, которые уже соответствуют правилам, и для каждой взять среднюю (центральную) страницу.
- Сумма этих страниц и является ответом.
💡 Идея
Для проверки корректности можно обходить последовательность и накапливать множество страниц, которые должны были уже встретиться раньше.
Если мы наткнемся на одну из них позже зависимой страницы, это нарушение!
📘 Часть II. Условие задачи
Теперь рассмотрим некорректные последовательности страниц.
Их нужно перестроить согласно правилам и взять сумму центральных страниц из корректных порядков.
💡 Идея
Это задача на топологическую сортировку.
- Правила определяют DAG (граф без циклов).
Читать дальше →
ответить
Задача 4-го дня Advent of Code — Ceres Search.
📌 Часть I. Условие задачи
Нам дано поле из символов. Нужно найти все вхождения слова "XMAS".
Слово может быть записано:
- по горизонтали,
- по вертикали,
- по диагонали,
- в обратном порядке,
- поверх других слов (т.е. вхождения могут перекрываться).
💡 Идея
Для поиска всех таких слов:
- Перебираем каждую ячейку как потенциальную стартовую.
- Из неё идём во все
8 направлений (вверх, вниз, вправо, влево, и 4 диагонали).
- Читаем
4 символа в этом направлении.
- Сравниваем полученное слово с
"XMAS".
📌 Часть II. Условие задачи
Теперь требуется найти не само слово XMAS, а X-образное расположение двух слов "MAS" вокруг символа "A".
Пример расположения:
M . S
Читать дальше →
ответить
Ссылка на задачу с LeetCode — 2179. Count Good Triplets in an Array.
📘 Условие задачи
Даны два массива nums1 и nums2, являющиеся перестановками чисел от 0 до n-1.
Нужно найти количество хороших троек (x, y, z), таких что:
- индексы этих значений возрастают в обоих массивах:
pos1(x)<pos1(y)<pos1(z) и pos2(x)<pos2(y)<pos2(z),- где
pos1(v) и pos2(v) — позиция значения v в nums1 и nums2 соответственно.
📌 Пример
- Вход:
nums1 = [2,0,1,3], nums2 = [0,1,2,3]
- Выход:
1
- Пояснение:
- Существуют 4 тройки, удовлетворяющие порядку в
nums1:
(2,0,1), (2,0,3), (2,1,3), (0,1,3)
- Из них только
(0,1,3) также удовлетворяет порядку в nums2.
💡 Идея
Рассматриваем каждое число как средний элемент потенциальной хорошей тройки.
Если знать, сколько подходящих чисел было до него и после него, можно посчитать количество троек с этим числом посередине.
Читать дальше →
ответить
Задача третьего дня Advent of Code — Mull It Over.
📘 Часть I. Описание задачи
- В дампе памяти содержатся команды вида
mul(X,Y), где X и Y — это числа от 1 до 999.
- Такие команды представляют собой простое умножение двух чисел.
- Однако память повреждена, и в тексте могут встречаться невалидные команды
(например: "mul(4*," "mul ( 2 , 3 )" и т.п.).
Необходимо выделить все корректные mul(X,Y) и подсчитать сумму произведений.
💡 Идея
Парсим только строки, точно соответствующие регулярному выражению "mul(\d{1,3},\d{1,3})", остальные пропускаем. После чего результат каждого умножения суммируем.
📘 Часть II. Описание задачи
Кроме mul, в дампе встречаются do() и don't():
do() включает обработку muldon't() отключает
По умолчанию mul разрешён. Надо подсчитать только те mul, которые активны в момент встречи.
💡 Идея
Читать дальше →
ответить
Задача второго дня Advent of Code — Red-Nosed Reports.
📘 Часть I. Описание задачи
Имеется множество отчётов, каждый из которых представляет собой последовательность целых чисел — уровней. Отчёт считается безопасным, если:
- Все уровни строго возрастают или строго убывают.
- Разность между любыми двумя соседними уровнями по модулю составляет от 1 до 3 включительно.
Пример безопасных отчётов:
Пример небезопасных отчётов:
1 2 5 9 # шаг больше 35 4 4 1 # не строго убывает
💡 Идея
Необходимо пройтись по каждой последовательности и проверить, являются ли все пары элементов:
- либо строго возрастающими (
a < b)
- либо строго убывающими (
a > b)
- и при этом |a - b| <= 3
Если хотя бы одна из этих проверок не выполняется — отчёт считается небезопасным.
Читать дальше →
ответить
100 задач с LeetCode мы уже обозрели. Пора переходить к более тяжёлым наркотикам.
Дальше будем смотреть на задачи из последнего Advent of Code.
Задача первого дня — Historian Hysteria несложная и затравочная 😻.
📘 Условие части I
Даны два списка целых чисел одинаковой длины. Необходимо оценить, насколько они различаются.
Для этого:
- Сопоставим наименьшее число из левого списка с наименьшим числом из правого.
- Затем второе по величине — со вторым по величине, и так далее.
- Для каждой пары чисел вычисляется расстояние между ними — это модуль разности.
- Все такие расстояния суммируются, и результат отражает общее расхождение между списками.
Пример:
- Левый список:
3 4 2 1 3 3
- Правый список:
4 3 5 3 9 3
После сопоставления по возрастанию:
- Пары:
(1, 3), (2, 3), (3, 3), (3, 4), (3, 5), (4, 9)
- Расстояния:
2, 1, 0, 1, 2, 5
- Сумма расстояний:
2 + 1 + 0 + 1 + 2 + 5 = 11
Читать дальше →
ответить
Условие задачи — 2874. Maximum Value of an Ordered Triplet II.
📄 Описание задачи
Дан массив целых чисел nums (индексация с нуля).
Нужно найти максимум выражения (nums[i]-nums[j])·nums[k] среди всех троек индексов i < j < k.
Если все такие значения отрицательны, вернуть 0.
💡 Идея
Выражение (nums[i]-nums[j])·nums[k] будет наибольшим, при фиксированном k, если:
- Число
nums[i] наибольшее
- Разность
nums[i]-nums[j] максимальна
Значит, на каждом шаге мы можем поддерживать максимальное значение разности (nums[i]-nums[j]) до текущего индекса и умножать его на nums[k], обновляя лучший результат.
🔍 Детали подхода
- Идем по массиву слева направо. На каждом шаге:
max_val хранит максимум из всех предыдущих чисел (nums[..i]);max_diff — максимум nums[i]-nums[j] на текущий момент;- умножаем
max_diff на текущий nums[k] и обновляем best.
- Всё делается за один проход, без дополнительных структур данных.
⏱️ Асимптотика
- Время:
O(n) — один проход по массиву
- Память:
O(1) — используются только 3 переменные
🧾 Исходный код
impl Solution {
pub fn maximum_triplet_value(nums: Vec<i32>) -> i64 {
nums.into_iter().fold((0i64, 0, 0), |(best, max_diff, max_val), x| (
best.max(x as i64 * max_diff as i64),
max_diff.max(max_val - x),
max_val.max(x),
)).0
}
}
Tags: #rust #algorithms #greedy
ответить
Ссылка на задачу — 2140. Solving Questions With Brainpower.
📋 Описание задачи
- Дан вектор
questions (questions[i] = [pointsi, brainpoweri]).
- Вы проходите тест, состоящий из последовательности вопросов.
- Если вы решаете вопрос
i, то зарабатываете pointsi баллов, но пропускаете следующие brainpoweri вопросов.
- Вопросы можно пропускать
- Нужно определить, максимальное количество баллов, которое можно набрать, действуя оптимально.
📌 Пример:
- Вход:
questions = [[3, 2], [4, 3], [4, 4], [2, 5]]
- Размышления:
- Если решить вопрос
0, вы получите 3 очка и пропустите вопросы 1 и 2, перейдёте сразу к 3 → итого: 3 + 2 = 5.
- Если пропустить
0 и решить 1, вы получите 4 очка и пропустите 2 и 3 → итого: 4.
- Если пропустить
0 и 1, решить 2 → получите 4 очка, но пропустите 3 → итого: 4.
- Если пропустить
0–2 и решить 3 → получите 2 очка.
🔎 Оптимальная стратегия: решить вопросы 0 и 3, что даст нам 5 баллов на экзамене.
- 👉 Ответ:
5.
💡 Идея
Читать дальше →
ответить
Ссылка на задачу — 2551. Put Marbles in Bags.
📌 Описание задачи
- Дан массив
weights, где weights[i] — вес i-го куска мрамора.
- Требуется разделить все куски на
k непустых мешков, соблюдая следующие правила:
- Каждый мешок содержит хотя бы один кусок.
- Если в мешке есть куски с индексами
i и j, то все элементы между ними также должны входить в этот мешок.
- Стоимость мешка — это сумма весов первого и последнего куска в нём, то есть:
weights[i] + weights[j].
- Нужно вернуть разность между максимально возможной и минимально возможной общей стоимостью всех
k мешков.
💡 Идея
При разбиении на k подряд идущих мешков мы делаем k - 1 разрез между кусками.
Каждый разрез влияет на итоговую сумму добавлением пары вида weights[i] + weights[i+1],
где i — индекс последнего элемента в предыдущем мешке.

Следовательно, вся задача сводится к выбору k - 1 пар соседних кусков, которые:
- минимизируют сумму (для минимального варианта),
- максимизируют сумму (для максимального варианта).
Читать дальше →
ответить
Ссылка на задачу — 763. Partition Labels.
📄 Описание задачи
- Дана строка
s, состоящая только из строчных латинских букв.
- Нужно разбить строку на как можно большее количество подстрок, таких что каждая буква встречается не более чем в одной подстроке.
- После разбиения объединение всех подстрок в порядке следования должно дать исходную строку.
- Например, для строки
"ababcc" корректное разбиение: ["abab", "cc"].
А такие варианты, как ["aba", "bcc"] или ["ab", "ab", "cc"] — недопустимы, потому что буквы повторяются в нескольких частях.
- Нужно вернуть список размеров всех полученных подстрок.
💡 Идея
Каждая буква должна присутствовать в одной части.
Значит, можно рассматривать все буквы как интервалы [первая позиция, последняя позиция].
Теперь задача сводится к жадному объединению перекрывающихся интервалов: как только текущий интервал завершился, мы фиксируем подстроку.
🔍 Детали подхода
- Проходим по строке один раз, чтобы:
- определить первую и последнюю позицию каждой буквы;
- зафиксировать порядок появления символов.
- Затем проходим по символам алфавита в порядке первого появления:
Читать дальше →
ответить
Условие задачи — 2503. Maximum Number of Points From Grid Queries.
📘 Условие задачи
- Дана матрица
grid размером m × n и массив целых чисел queries, каждый из которых представляет пороговое значение.
- Для каждого запроса
queries[i] необходимо определить, сколько уникальных ячеек можно достичь, начиная с (0, 0), если разрешено:
- двигаться вверх, вниз, влево и вправо;
- заходить только в те ячейки, значение которых строго меньше
queries[i];
- Нужно вернуть массив
result, где result[i] — это общее количество очков, полученных для queries[i].
💡 Идея
Вместо того чтобы запускать поиск заново для каждого запроса, можно:
- выполнить один глобальный обход BFS, начиная с
(0, 0);
- посещать ячейки по возрастанию их значений (с помощью min-heap);
- на лету отвечать на все запросы, чьё значение не превышает текущей ячейки.
Такой метод за 1 проход отвечает сразу на все запросы.
🛠️ Детали реализации
- Сохраняем исходные индексы запросов и сортируем их по значениям.
Читать дальше →
ответить
Ссылка на задачу — 2780. Minimum Index of a Valid Split.
📘 Описание задачи
- Дан массив целых чисел
nums, в котором гарантированно существует один доминирующий элемент
(то есть такой элемент, который встречается чаще, чем половина длины массива).
- Необходимо найти наименьший индекс
i, такой что массив можно разделить на две части:
nums[0],..,nums[i] и nums[i+1],..,nums[n-1],- и обе части будут иметь одинаковый доминирующий элемент.
- Если такого разделения не существует — вернуть
-1.
💡 Идея
Для эффективного поиска доминирующего элемента хорошо подходит алгоритм большинства голосов Бойера — Мура.
Зная доминирующий элемент, можно пройти по массиву и в каждой возможной точке разделения отслеживать:
- Сколько раз этот элемент встречался слева;
- Сколько осталось справа;
- Затем проверяется, является ли он доминирующим в обеих частях.
🔍 Детали подхода
- Применяем алгоритм голосования большинства для нахождения доминанты.
- Подсчитываем точное количество его вхождений, чтобы использовать для отслеживания остатка справа.
Читать дальше →
ответить
Ссылка на задачу — 2033. Minimum Operations to Make a Uni-Value Grid.
📌 Описание задачи
Дан двумерный массив grid размером m x n, а также число x.
За одну операцию можно прибавить или
Читать дальше →
ответить
Ссылка на задачу — 3394. Check if Grid can be Cut into Sections.
📌 Описание задачи
Дано квадратное поле n×n, в котором размещены непересекающиеся прямоугольники.
Необходимо определить, можно ли сделать две горизонтальные или две вертикальные разрезки, чтобы:
- В каждой из трёх частей оказалось хотя бы по одному прямоугольнику.
- Каждый прямоугольник остался ровно в одной части.
Если такие разрезки возможны, вернуть true, иначе — false.
Пример
- Входные данные:
n = 5, rectangles = [[1,0,5,2],[0,2,2,4],[3,2,5,3],[0,4,4,5]]
- Ответ:
true
- Визуальное пояснение:
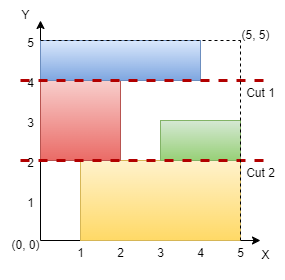
💡 Идея
Поскольку прямоугольники не пересекаются, возможные разрезки должны полностью разделять их на независимые группы.
Мы спроектируем прямоугольники на каждую ось. Если полученные отрезки отсортировать по координатам и просканировать их, можно определить количество неперекрывающихся сегментов, это позволит понять, возможно ли корректное разбиение.
Читать дальше →
ответить
Ссылка на задачу — 3169. Count Days Without Meetings.
📌 Описание задачи
- Данo
days — количество дней, в течение которых сотрудник доступен для работы.
- Также дан массив
meetings, где meetings[i] = [starti, endi] обозначает дни проведения встречи.
Нужно посчитать количество дней, когда сотрудник свободен от встреч и может работать.
💡 Идея
Мы сортируем встречи по дню начала, чтобы затем обходить их в порядке возрастания.
Это позволяет использовать метод заметания линии как эффективный способ вычислить количество свободных дней между встречами.
🚀 Детали подхода
1️⃣ Сортируем встречи по начальной дате.
2️⃣ Проходим по списку встреч, отслеживая next_free (следующий свободный день).
3️⃣ Подсчитываем разрывы между next_free и началом следующей встречи.
4️⃣ Обновляем next_free после каждой встречи, сдвигая его на день после её окончания.
5️⃣ Добавляем свободные дни после последней встречи.
⏳ Асимптотика
-
Время:
O(n·logn)
O(n·logn) на сортировку.O(n) на обход.
-
Память:
O(1)
- Используем только несколько переменных.
💻 Исходный код
impl Solution {
pub fn count_days(days: i32, mut meetings: Vec<Vec<i32>>) -> i32 {
meetings.sort_unstable_by_key(|meet| meet[0]);
let (next_free, free_count) = meetings.into_iter()
.fold((1, 0), |(next_free, free_count), meet| {
let [start, end] = meet[..2] else { unreachable!("bad meet format") };
let gap = (start - next_free).max(0);
let next_free = next_free.max(end + 1);
(next_free, free_count + gap)
});
free_count + (days - next_free + 1).max(0)
}
}
Tags: #rust #algorithms #counting
ответить
Ссылка на задачу — 2115. Find All Possible Recipes from Given Supplies.
В этой задаче для эффективного решения важно не только выбрать эффективный алгоритм, но и аккуратно разложить строки по необходимым структурам данных, избежать лишних копирований и обеспечить ясную картину ownership'a за объектами.
📌 Описание задачи
- У нас есть список рецептов, каждому из которых соответствует список ингредиентов.
- Некоторые ингредиенты могут быть другими рецептами, а некоторые — изначально доступны (входят в список запасов).
- Нужно определить, какие рецепты можно приготовить, имея начальные запасы и возможность использовать приготовленные рецепты.
💡 Идея
Используем рекурсивный DFS для проверки доступности рецептов.
Чтобы избежать повторных вычислений, применяем мемоизацию (кеширование уже проверенных результатов).
Вместо хранения графа явным образом, мы используем индексирование рецептов и проходим по их списку ингредиентов.
🔍 Детали подхода
- Предобработка входных данных:
- Создаём хеш-таблицу для быстрого доступа к индексу каждого рецепта.
- Добавляем начальные запасы в кеш доступных ингредиентов.
Читать дальше →
ответить
Ссылка на задачу — 3108. Minimum Cost Walk in Weighted Graph.
📌 Описание задачи
- Дан неориентированный взвешенный граф с
n вершинами и m рёбрами.
- Каждое ребро представлено тройкой
[u, v, w], означающей, что существует ребро между u и v с весом w.
- Определим стоимость пути между двумя вершинами как битовое
AND всех рёбер, пройденных на пути (вершинам в таком пути разрешено повторяться).
- Для каждого запроса
[s, t] требуется найти минимальную AND-стоимость пути между s и t.
- Если пути не существует, ответ
-1.
Пример
- Входные данные:
n = 5; edges = [[0,1,7],[1,3,7],[1,2,1]]; query = [[0,3],[3,4]]
- Результаты:
[1, -1]
- Объяснение:
- Наилучший путь от
0 до 3: 0 → 1 → 2 → 1 → 3.
- Путей из
3 в 4 не существует.
- Графическая интерпретация:
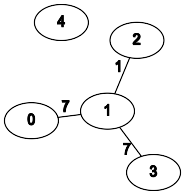
💡 Идея
- Так как каждое новое ребро пути его стоимость не увеличивает, то внутри каждой компоненты связности стоимость минимального пути будет одинаковой (достаточно определить путь, проходящий через все рёбра компоненты связности).
Читать дальше →
1 ответ
Ссылка на задачу — 3191. Minimum Operations to Make Binary Array Elements Equal to One I.
📌 Описание задачи
- Дан массив
nums, состоящий из 0 и 1.
- Можно переворачивать любые три подряд идущих элемента (
0 становится 1, а 1 — 0).
- Нужно найти минимальное количество операций, чтобы сделать все элементы
1. Если это невозможно, вернуть -1.
Пример:
- Вход:
nums = [0,1,1,1,0,0]
- Выход:
3
- Объяснение: Можно выполнить следующие операции:
1️⃣ Выбираем элементы с индексами [0,1,2]. Новый массив: [1,0,0,1,0,0]
2️⃣ Выбираем элементы с индексами [1,2,3]. Новый массив: [1,1,1,0,0,0]
3️⃣ Выбираем элементы с индексами [3,4,5]. Новый массив: [1,1,1,1,1,1] ✅
💡 Идея
- Будем искать необходимые перевороты слева-направо (это валидно, ибо 3-перевороты коммутируют друг с другом).
- Вместо непосредственного изменения
nums будем использовать битовый сдвиговый регистр flip_state (на 2 бита) для отслеживания переворотов вперед на 2 значения.
Читать дальше →
ответить
Ссылка на задачу — 2401. Longest Nice Subarray.
📌 Описание задачи
Дан массив nums, состоящий из целых чисел.
Нужно найти наибольший подмассив, в котором ни одна пара чисел не имеет общих установленных битов
(т.е. их побитовое И (&) равно 0).
Пример
- 📥 Вход:
nums = [1, 3, 8, 48, 10]
- 📤 Выход:
3
- 🔍 Пояснение: Наибольший "красивый" подмассив:
[3, 8, 48], так как:
3 & 8 = 03 & 48 = 08 & 48 = 0- Никакой больший подмассив не удовлетворяет условиям.
💡 Идея
Будем решать задачу в чистом функциональном стиле, используя технику скользящего окна.
- Расширяем окно вправо, если
nums[right] не конфликтует с текущим битовым множеством.
- Сжимаем окно слева, если появляется конфликт.
- Отслеживаем текущее битовое множество (
cur_bitset), обновляя его при изменении окна.
Читать дальше →
1 ответ
Страница
1
2
3
4
5
