Ссылка на задачу — 2033. Minimum Operations to Make a Uni-Value Grid.
📌 Описание задачи
Дан двумерный массив grid размером m x n, а также число x.
За одну операцию можно прибавить или вычесть x из любого элемента массива.
Нужно найти минимальное количество операций, необходимых для приведения всех элементов grid к одному значению.
Если это невозможно — вернуть -1.
Пример
- Вход:
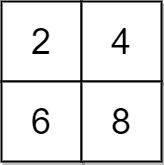
grid = [[2,4],[6,8]]; x = 2
- Выход:
4
- Пояснение: Можно привести все элементы к 4 за 4 операции
💡 Идея
- Чтобы все элементы стали равными, их остатки при делении на
x должны быть одинаковыми.
- После проверки этого условия задача сводится к поиску оптимального целевого значения, минимизирующего количество операций.
- Это может быть сделано путём однократной проверки всех значений как возможных опорных величин в отсортированном порядке для эффективного динамического расчёта числа операций с помощью счётчиков баланса.
ops = sum_balance − cells_balance ∗ val

- Вместо сортировки всех элементов (
O(N·log N)), мы можем использовать счётчик частот,
что ускоряет вычисления до O(N + K).
⚙️ Детали подхода
- Строим частотный массив
- Проверяем, что все числа имеют одинаковый остаток при делении на
x.
- Подсчитываем количество вхождений каждого числа, отмасштабированного к
val / x, чтобы избавиться от влияния x.
- Находим минимальный и максимальный индексы среди встречающихся значений, чтобы соответствующим образом вырезать минимально необходимый сектор из вектора частот.
- Ищем оптимальную опорную величину
- Отслеживаем балансные счётчики, проходя по отсортированным значениям в векторе частот.
- Вычисляем динамически количество операций, поочерёдно проверяя все возможные опорные точки.
- Возвращаем минимальное количество операций
- Если условия выполнимости не нарушены — выводим ответ.
- Иначе — возвращаем
-1.
⏳ Асимптотика
- Временная сложность:
O(N + K)
O(N) — построение counters_grid (один проход по массиву).O(K) — итерация по релевантному диапазону значений,
где K ≤ 10⁴ — количество возможных значений в сетке.
- Пространственная сложность:
O(K)
- используем частотный массив вместо хранения всех чисел.
💻 Исходный код
impl Solution {
pub fn min_operations(grid: Vec<Vec<i32>>, x: i32) -> i32 {
let total_cells = grid.len() * grid[0].len();
// Get frequency counters for scaled values
let mut counters_grid = match Self::get_counters_grid(grid, x) {
Some(counters) => counters,
None => return -1, // Impossible to make all values equal
};
// Compute initial sum of differences
let mut sum_balance = counters_grid.iter()
.enumerate()
.map(|(value, &count)| value * count)
.sum::<usize>();
let mut cells_balance = total_cells;
let mut min_ops = sum_balance;
// Iterate over the frequency counter and adjust balances
counters_grid.into_iter()
.enumerate()
.map(|(value, count)| {
sum_balance -= 2 * value * count;
cells_balance -= 2 * count;
sum_balance - cells_balance * value
})
.min()
.unwrap() as _
}
// Converts a 2D grid into a frequency counter for scaled values.
// The transformation is impossible when at least two values in the grid have different remainders when divided by x.
// Returns None if transformation is impossible.
fn get_counters_grid(grid: Vec<Vec<i32>>, x: i32) -> Option<Vec<usize>> {
const MAX_INDEX: usize = 10_000; // Upper bound for value indices
let mut counters_grid = vec![0; MAX_INDEX + 1];
let mod_base = grid[0][0] % x;
let (mut min_index, mut max_index) = (MAX_INDEX, 0);
for row in grid {
for val in row {
if val % x != mod_base {
return None; // Impossible transformation
}
let index = (val / x) as usize;
max_index = max_index.max(index + 1);
min_index = min_index.min(index);
counters_grid[index] += 1;
}
}
// Trim the counters grid to the relevant range
Some(counters_grid[min_index..max_index].to_vec())
}
}
Tags: #rust #algorithms #optimization