Ссылка на задачу — 3108. Minimum Cost Walk in Weighted Graph.
📌 Описание задачи
- Дан неориентированный взвешенный граф с
n вершинами и m рёбрами.
- Каждое ребро представлено тройкой
[u, v, w], означающей, что существует ребро между u и v с весом w.
- Определим стоимость пути между двумя вершинами как битовое
AND всех рёбер, пройденных на пути (вершинам в таком пути разрешено повторяться).
- Для каждого запроса
[s, t] требуется найти минимальную AND-стоимость пути между s и t.
- Если пути не существует, ответ
-1.
Пример
- Входные данные:
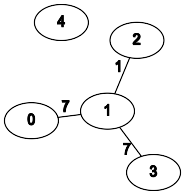
n = 5; edges = [[0,1,7],[1,3,7],[1,2,1]]; query = [[0,3],[3,4]]
- Результаты:
[1, -1]
- Объяснение:
- Наилучший путь от
0 до 3: 0 → 1 → 2 → 1 → 3.
- Путей из
3 в 4 не существует.
- Графическая интерпретация:
💡 Идея
- Так как каждое новое ребро пути его стоимость не увеличивает, то внутри каждой компоненты связности стоимость минимального пути будет одинаковой (достаточно определить путь, проходящий через все рёбра компоненты связности).
Читать дальше →
1 ответ
Очередная задача — 2375. Construct Smallest Number From DI String сходу выглядит переборной, но может быть эффективно реализована за счёт использования графовых алгоритмов.
📝 Описание задачи
Дан строковый шаблон pattern, состоящий из символов I и D.
Необходимо построить лексикографически наименьшее число длины n+1, используя цифры от 1 до 9 без повторений, которое соответствует следующим требованиям:
'I' (увеличение) на позиции i → требует, чтобы num[i] < num[i+1].'D' (уменьшение) на позиции i → требует, чтобы num[i] > num[i+1].
💡 Идея
Рассмотрим шаблон как ориентированный граф, где каждая позиция (i) — это вершина.
- Если
pattern[i] == 'I', создаём ребро i → i+1.
- Если
pattern[i] == 'D', создаём ребро i+1 → i.
После построения графа можно выполнить топологическую сортировку, начиная с вершин с нулевой степенью захода.
Чтобы гарантировать лексикографически наименьший порядок, обрабатываем вершины через приоритетную очередь (Min-Heap).
⚙️ Детали подхода
Читать дальше →
ответить
Следуюшая задача для нашего обзора - 827. Making A Large Island.
Интересный способ для постобработки результатов стандартного поиска в графе.
📌 Описание Задачи
Дан n × n бинарный массив grid, где 1 — это суша, а 0 — вода.
Можно изменить ровно один 0 на 1, после чего необходимо найти размер самого большого острова.
Остров — это группа соседних единичек (соседи считаются по 4-м направлениям).

💡 Идея
1️⃣ Сначала находим и маркируем все острова, присваивая им уникальные ID.
2️⃣ Затем проверяем каждую клетку 0 и считаем, насколько большой станет остров, если заменить её на 1.
🛠️ Детали Подхода
- Маркируем острова с помощью
BFS
- Обход в ширину помечает все клетки острова уникальным
ID (начиная с 2).
- Запоминаем размер каждого острова.
Читать дальше →
ответить
Задача - 2493. Divide Nodes Into the Maximum Number of Groups.
📌 Постановка задачи
Дан неориентированный граф с n вершинами, возможно несвязный. Требуется разбить вершины на m групп, соблюдая условия:
✔ Каждая вершина принадлежит ровно одной группе.
✔ Если вершины соединены ребром [a, b], то они должны находиться в смежных группах (|group[a] - group[b]| = 1).
✔ Найти максимальное количество таких групп m.
✔ Вернуть -1, если разбиение невозможно.
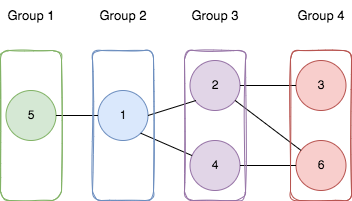
💡 Идея
- Граф можно корректно разбить на группы ↔ он двудольный.
- Максимальное количество групп связано с максимальной глубиной BFS в каждой компоненте.
- Мы проверяем BFS из каждой вершины, чтобы найти наилучший возможный корень для каждой компоненты.
🔍 Детали подхода
- Строим граф в виде списка смежности.
- Запускаем
BFS из каждой вершины (а не только из одной в компоненте) для:
- Проверки двудольности (по уровням
BFS).
- Поиска максимальной глубины
BFS (max_level).
- Определения уникального идентификатора компоненты (
min_index).
Читать дальше →
ответить
Следующая задача для разбора - 1462. Course Schedule IV
✨ Описание задачи
У нас есть numCourses курсов, пронумерованных от 0 до numCourses - 1.
Даны:
- Массив
prerequisites, где prerequisites[i] = [a, b] указывает, что курс a необходимо пройти перед курсом b.
- Массив запросов queries, где
queries[j] = [u, v] спрашивает: является ли курс u предшественником курса v.
Нужно вернуть массив булевых значений, где для каждого запроса ответ — true, если курс u является прямым или косвенным предшественником курса v; или false, если нет.
💡 Идея
Представим зависимости курсов в виде графа, где вершины — это курсы, а ребра указывают на зависимости между ними. Наша цель — определить, существует ли путь между двумя вершинами графа. Для этого можно использовать алгоритм Флойда-Уоршелла, чтобы вычислить транзитивное замыкание графа.
🛠️ Подробности подхода
- Инициализация матрицы зависимостей: Создаем булевую матрицу
n x n, где dep_matrix[i][j] обозначает, что курс i является предшественником курса j.
- Заполнение прямых зависимостей: На основе массива
prerequisites отмечаем прямые зависимости в матрице.
Читать дальше →
ответить
В очередной задаче для обзора - 802. Find Eventual Safe States нам предстоит найти вершины, не попадающие в циклы графа.
📋 Описание задачи
Нужно определить безопасные вершины в ориентированном графе.
- Безопасная вершина — это такая вершина, из которой невозможно попасть в цикл. Если из вершины можно попасть только в терминальные вершины или другие безопасные, она считается безопасной.
- Граф представлен в виде списка смежности, где
graph[i] содержит все вершины, в которые можно попасть из вершины i.
- Вернуть необходимо список всех безопасных вершин в возрастающем порядке.

- Граф из примера имеет безопасными вершины:
[4,5,6]
💡 Идея
Задача решается с помощью обхода графа в глубину (DFS) и вектора состояний.
Каждому узлу присваивается одно из трёх состояний:
Unseen (ещё не обработан);Processing (в процессе обработки; узлы, являющиеся частью цикла, остаются в этом состоянии и после обработки);Safe (безопасный).
🔍 Детальное описание подхода
Читать дальше →
ответить
