Ссылка на задачу — 3108. Minimum Cost Walk in Weighted Graph.
📌 Описание задачи
- Дан неориентированный взвешенный граф с
n вершинами и m рёбрами.
- Каждое ребро представлено тройкой
[u, v, w], означающей, что существует ребро между u и v с весом w.
- Определим стоимость пути между двумя вершинами как битовое
AND всех рёбер, пройденных на пути (вершинам в таком пути разрешено повторяться).
- Для каждого запроса
[s, t] требуется найти минимальную AND-стоимость пути между s и t.
- Если пути не существует, ответ
-1.
Пример
- Входные данные:
n = 5; edges = [[0,1,7],[1,3,7],[1,2,1]]; query = [[0,3],[3,4]]
- Результаты:
[1, -1]
- Объяснение:
- Наилучший путь от
0 до 3: 0 → 1 → 2 → 1 → 3.
- Путей из
3 в 4 не существует.
- Графическая интерпретация:
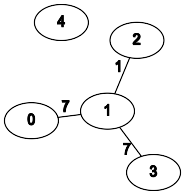
💡 Идея
- Так как каждое новое ребро пути его стоимость не увеличивает, то внутри каждой компоненты связности стоимость минимального пути будет одинаковой (достаточно определить путь, проходящий через все рёбра компоненты связности).
Читать дальше →
1 ответ
Ссылка на задачу — 2115. Find All Possible Recipes from Given Supplies.
В этой задаче для эффективного решения важно не только выбрать эффективный алгоритм, но и аккуратно разложить строки по необходимым структурам данных, избежать лишних копирований и обеспечить ясную картину ownership'a за объектами.
📌 Описание задачи
- У нас есть список рецептов, каждому из которых соответствует список ингредиентов.
- Некоторые ингредиенты могут быть другими рецептами, а некоторые — изначально доступны (входят в список запасов).
- Нужно определить, какие рецепты можно приготовить, имея начальные запасы и возможность использовать приготовленные рецепты.
💡 Идея
Используем рекурсивный DFS для проверки доступности рецептов.
Чтобы избежать повторных вычислений, применяем мемоизацию (кеширование уже проверенных результатов).
Вместо хранения графа явным образом, мы используем индексирование рецептов и проходим по их списку ингредиентов.
🔍 Детали подхода
- Предобработка входных данных:
- Создаём хеш-таблицу для быстрого доступа к индексу каждого рецепта.
- Добавляем начальные запасы в кеш доступных ингредиентов.
Читать дальше →
ответить
Ссылка на задачу — 2467. Most Profitable Path in a Tree.
📌 Описание задачи
Дано неориентированное корневое дерево с n узлами (нумерованными от 0 до n-1).
- У каждого узла есть врата, открытие которых может принести прибыль или потребовать затрат (
amount[i]).
- Алиса начинает движение от корня (
0) к какому-либо листу, выбирая максимально выгодный путь.
- Боб начинает движение из указанной вершины
bob и движется к корню (0).
- Если Алиса и Боб одновременно посещают узел, они делят
стоимость/прибыль пополам.
Нужно найти максимальный чистый доход Алисы при оптимальном выборе пути.
💭 Идея
Вместо раздельного запуска BFS для поиска пути Боба и последующего прохода динамического программирования по узлам дерева, мы решим задачу одним рекурсивным DFS-проходом.
Для каждого узла будем вычислять:
alice_profit[node] – максимальный доход, который может собрать Алиса из поддерева.bob_distance[node] – расстояние на пути Боба до этой вершины.- Если Боб раньше доберётся до узла → Алиса ничего не получит.
Читать дальше →
ответить
В очередной задаче для обзора - 802. Find Eventual Safe States нам предстоит найти вершины, не попадающие в циклы графа.
📋 Описание задачи
Нужно определить безопасные вершины в ориентированном графе.
- Безопасная вершина — это такая вершина, из которой невозможно попасть в цикл. Если из вершины можно попасть только в терминальные вершины или другие безопасные, она считается безопасной.
- Граф представлен в виде списка смежности, где
graph[i] содержит все вершины, в которые можно попасть из вершины i.
- Вернуть необходимо список всех безопасных вершин в возрастающем порядке.

- Граф из примера имеет безопасными вершины:
[4,5,6]
💡 Идея
Задача решается с помощью обхода графа в глубину (DFS) и вектора состояний.
Каждому узлу присваивается одно из трёх состояний:
Unseen (ещё не обработан);Processing (в процессе обработки; узлы, являющиеся частью цикла, остаются в этом состоянии и после обработки);Safe (безопасный).
🔍 Детальное описание подхода
Читать дальше →
ответить
