Условие задачи — 2503. Maximum Number of Points From Grid Queries.
📘 Условие задачи
- Дана матрица
grid размером m × n и массив целых чисел queries, каждый из которых представляет пороговое значение.
- Для каждого запроса
queries[i] необходимо определить, сколько уникальных ячеек можно достичь, начиная с (0, 0), если разрешено:
- двигаться вверх, вниз, влево и вправо;
- заходить только в те ячейки, значение которых строго меньше
queries[i];
- Нужно вернуть массив
result, где result[i] — это общее количество очков, полученных для queries[i].
💡 Идея
Вместо того чтобы запускать поиск заново для каждого запроса, можно:
- выполнить один глобальный обход BFS, начиная с
(0, 0);
- посещать ячейки по возрастанию их значений (с помощью min-heap);
- на лету отвечать на все запросы, чьё значение не превышает текущей ячейки.
Такой метод за 1 проход отвечает сразу на все запросы.
🛠️ Детали реализации
- Сохраняем исходные индексы запросов и сортируем их по значениям.
Читать дальше →
ответить
Следуюшая задача для нашего обзора - 827. Making A Large Island.
Интересный способ для постобработки результатов стандартного поиска в графе.
📌 Описание Задачи
Дан n × n бинарный массив grid, где 1 — это суша, а 0 — вода.
Можно изменить ровно один 0 на 1, после чего необходимо найти размер самого большого острова.
Остров — это группа соседних единичек (соседи считаются по 4-м направлениям).

💡 Идея
1️⃣ Сначала находим и маркируем все острова, присваивая им уникальные ID.
2️⃣ Затем проверяем каждую клетку 0 и считаем, насколько большой станет остров, если заменить её на 1.
🛠️ Детали Подхода
- Маркируем острова с помощью
BFS
- Обход в ширину помечает все клетки острова уникальным
ID (начиная с 2).
- Запоминаем размер каждого острова.
Читать дальше →
ответить
Задача - 2493. Divide Nodes Into the Maximum Number of Groups.
📌 Постановка задачи
Дан неориентированный граф с n вершинами, возможно несвязный. Требуется разбить вершины на m групп, соблюдая условия:
✔ Каждая вершина принадлежит ровно одной группе.
✔ Если вершины соединены ребром [a, b], то они должны находиться в смежных группах (|group[a] - group[b]| = 1).
✔ Найти максимальное количество таких групп m.
✔ Вернуть -1, если разбиение невозможно.
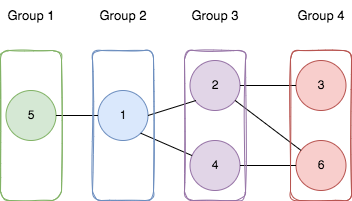
💡 Идея
- Граф можно корректно разбить на группы ↔ он двудольный.
- Максимальное количество групп связано с максимальной глубиной BFS в каждой компоненте.
- Мы проверяем BFS из каждой вершины, чтобы найти наилучший возможный корень для каждой компоненты.
🔍 Детали подхода
- Строим граф в виде списка смежности.
- Запускаем
BFS из каждой вершины (а не только из одной в компоненте) для:
- Проверки двудольности (по уровням
BFS).
- Поиска максимальной глубины
BFS (max_level).
- Определения уникального идентификатора компоненты (
min_index).
Читать дальше →
ответить
В нашей новой задаче - 1765. Map of Highest Peak продолжим закреплять работу с семейством простых графовых алгоритмов.
📜 Описание задачи
Вам дана матрица isWater размером m×n, где:
isWater[i][j] == 1 указывает, что клетка — это вода.isWater[i][j] == 0 указывает, что клетка — это суша.
Требуется назначить высоты каждой клетке таким образом, чтобы:
- Высота каждой клетки была неотрицательной.
- Высота любой клетки с водой была равна 0.
- Абсолютная разница высот у соседних клеток не превышала 1.
- Максимальная высота в назначенной карте была как можно больше.
💡 Идея
Мы используем поиск в ширину с несколькими источниками (multi-source BFS), начиная с клеток воды (высота 0).
На каждом шаге ближайшие клетки суши получают высоту на 1 больше текущей.
Этот метод гарантирует, что все клетки суши получают наилучшую из возможных высот, что приводит к максимизации самой высокой высоты в матрице.
🛠 Подробности подхода
- Инициализация:
- Создаём очередь и добавляем в неё все клетки воды, помечая их высотой
0.
Читать дальше →
ответить
