Ссылка на задачу — 2467. Most Profitable Path in a Tree.
📌 Описание задачи
Дано неориентированное корневое дерево с n узлами (нумерованными от 0 до n-1).
- У каждого узла есть врата, открытие которых может принести прибыль или потребовать затрат (
amount[i]).
- Алиса начинает движение от корня (
0) к какому-либо листу, выбирая максимально выгодный путь.
- Боб начинает движение из указанной вершины
bob и движется к корню (0).
- Если Алиса и Боб одновременно посещают узел, они делят
стоимость/прибыль пополам.
Нужно найти максимальный чистый доход Алисы при оптимальном выборе пути.
💭 Идея
Вместо раздельного запуска BFS для поиска пути Боба и последующего прохода динамического программирования по узлам дерева, мы решим задачу одним рекурсивным DFS-проходом.
Для каждого узла будем вычислять:
alice_profit[node] – максимальный доход, который может собрать Алиса из поддерева.bob_distance[node] – расстояние на пути Боба до этой вершины.- Если Боб раньше доберётся до узла → Алиса ничего не получит.
Читать дальше →
ответить
Ссылка на задачу — 889. Construct Binary Tree from Preorder and Postorder Traversal.
📌 Описание задачи
Нам даны прямой (preorder) и обратный (postorder) обходы бинарного дерева.
Необходимо восстановить дерево по этим обходам.
Основные свойства обходов:
- Preorder (прямой обход):
[корень → левый → правый]
- Postorder (обратный обход):
[левый → правый → корень]
💡 Идея
Для построения дерева используем рекурсивный подход, основанный на двух ключевых наблюдениях:
- 1️⃣ Каждый новый узел получает значение из
preorder
→ так мы всегда сначала создаем корень поддерева.
- 2️⃣ Поддерево считается полностью построенным, когда его значение встречается в
postorder
→ это сигнал к завершению рекурсии.
🔍 Детали подхода
- Используем итераторы
Peekable<Iterator> для эффективного прохода по preorder и postorder.
- Берем значение из
preorder и создаем новый узел.
- Рекурсивно создаем левое поддерево, если
postorder пока не указывает на текущий корень.
Читать дальше →
ответить
Ссылка на задачу — 1028. Recover a Tree From Preorder Traversal.
📝 Описание задачи
Дано строковое представление бинарного дерева, полученное в порядке прямого обхода, где:
- Каждый узел записан в формате
Dashes + Value, где количество - (тире) указывает на глубину узла.
- Глубина корневого узла —
0, его дочерний узел имеет глубину 1, внуки — 2 и так далее.
- Если у узла есть только один ребёнок, то это всегда левый ребёнок.
Например для следующего дерева, представление будет таким: 1-2--3---4-5--6---7
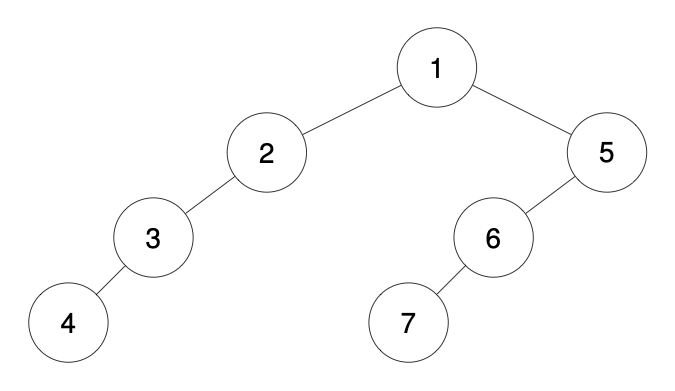
Необходимо восстановить бинарное дерево по этой строке и вернуть его корень.
💡 Идея
- Нам нужно восстановить бинарное дерево из его обхода с закодированными глубинами.
- Традиционное решение:
- разбить строку на токены (
Dashes + Value);
- затем рекурсивно собрать дерево по массиву токенов.
- Мы же сделаем чуть больше работы, и будем лениво разбирать представление на токены (вместо того, чтобы сразу сохранить их в
Vec)
Читать дальше →
ответить
Ссылка на задачу – 1261. Find Elements in a Contaminated Binary Tree.
📝 Описание задачи
Дано двоичное дерево, в котором:
- Корень всегда имеет значение
0.
- Для каждого узла со значением
x:
- Если есть левый потомок, то его значение
2 * x + 1.
- Если есть правый потомок, то его значение
2 * x + 2.
Значения всех узлов загрязнены (-1).
Нужно реализовать структуру FindElements, которая:
- Принимает корень «загрязнённого» дерева в конструкторе.
- Реализует
find(target) — метод, проверяющий существует ли узел с таким значением.
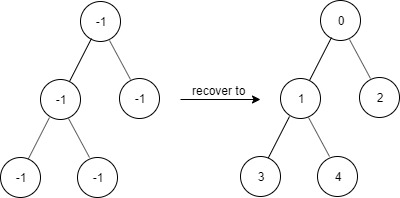
💡 Идея
Восстанавливать дерево не требуется!
Вместо этого мы вычисляем путь к узлу target, определяя его родителя и положение.
🔍 Детали подхода
- Поиск родителя (
parent):
Читать дальше →
ответить
